Выбор обобщенных координат

Определение числа степеней свободы системы

Напомним (подробнее см. прил. 1), что числом степеней свободы системы называется число независимых возможных перемещений этой системы. Число степеней свободы системы определяют следующим образом. Вначале у системы исключают одну степень свободы (для этого закрепляют точку, движущуюся по заданной линии, или закрепляют вращающееся тело). Если после этого подвижность системы будет полностью устранена, значит у системы одна степень свободы. Если же подвижность сохранится, то исключают еще одну степень свободы. И так далее до полной остановки системы. Число таких исключений равно числу степеней свободы системы.

Учитывая сказанное, легко убедиться, что система на рис. 1.1 имеет одну степень свободы, а системы на рис. 1.2 и 1.3 – две степени свободы.

Иногда в соответствии с условием задачи некоторые возможные перемещения системы в расчет не принимаются. Так, в примере 2 горизонтальные возможные перемещения точек A и D не учитываются, потому что по условию задачи эти точки движутся по вертикали.

Напомним, что обобщенными координатами называются независимые между собой переменные параметры системы, которые однозначно определяют положение тел и точек этой системы в любой момент времени. В качестве обобщенных координат обычно выбирают углы поворота тел системы или координаты ее точек. Начало и положительное направление отсчета каждой обобщенной координаты рекомендуется выбирать так, чтобы в процессе движения эти координаты возрастали. Если система имеет положение статического равновесия, то начало отсчета рекомендуется выбирать так, чтобы в положении статического равновесия все обобщенные координаты системы были равны нулю.

Во многих случаях выбор обобщенных координат определяется условием задачи. Если в задаче нужно найти ускорение а некоторой точки, движущейся вдоль оси x, то в качестве обобщенной координаты следует взять координату x этой точки, то есть q = x. Тогда искомое ускорение 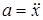. Если же в задаче требуется найти угловое ускорение e тела, вращающегося вокруг оси, то в качестве обобщенной координаты следует взять угол j поворота тела вокруг этой оси. Тогда искомое угловое ускорение .

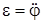Пример 1.1 (рис. 1.1)

В качестве обобщенной координаты системы можно выбрать координату s точки A, отсчитываемую вдоль линии ее движения от какой-либо неподвижной точки на этой линии в направлении движения точки A.

Если бы по условию задачи требовалось определить угловое ускорение барабана B, то в качестве обобщенной координаты системы следовало взять угол j поворота барабана, отсчитываемый от какого-либо начала отсчета в направлении вращения барабана.

Пример 1.2 (рис. 1.2)

Предполагая, что точки A и D движутся вниз, в качестве обобщенных координат системы следует взять x_A и x_D, отсчитываемые от оси y вниз. Если в результате решения задачи окажется, что (или ), то это будет означать, что точка A (или D) движется вверх.

Пример 1.3 (рис. 1.3)

Эта система имеет положение статического равновесия, в котором стержень AB совпадает с осью x, а сила тяжести G шарика D уравновешена силой упругости пружины. Напомним, что сила упругости пружины , где c – коэффициент жесткости пружины, 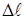– ее деформация в произвольном положении шарика D; l – деформация пружины в положении статического равновесия системы. Учитывая, что l = G / c, получим

F = G + cs. (а)

В качестве обобщенных координат системы в данном примере следует взять угол j поворота стержня AB и расстояние s шарика D от его положения, в котором деформация пружины равна l.

Дата добавления: 2014-12-07