Пример 1.11

Пример 1.10

Составим дифференциальные уравнения движения системы на рис. 1.1. Как указывалось ранее, система имеет одну степень свободы, за обобщенную координату взята величина s. Кинетическая энергия системы определяется по формуле (ж), обобщенная сила – формуле (б).

Найдем производные, входящие в уравнение (1.1): , так как s в T явно не входит; далее

.

Подставляя найденные результаты в уравнение (1.1), получим искомое уравнение движения системы

.

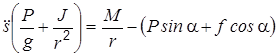Составим дифференциальные уравнения движения системы (рис. 1.2). Как указывалось, система имеет две степени свободы; за обобщенные координаты взяты величины x_A и x_D. Кинетическая энергия системы определяется формулой (и), обобщенные силы – формулами (в) и (г).

Найдем производные, входящие в уравнения (1.1):

Подставляя найденные результаты в уравнения (1.1), получим искомые уравнения движения системы

Дата добавления: 2014-12-07