Определение потенциальной энергии системы

Потенциальная энергия, как известно, определяется с точностью до постоянного слагаемого. Поэтому потенциальную энергию системы в некотором наперед выбранном положении всегда можно принять равной нулю. Обычно полагают равной нулю потенциальную энергию системы в положении, где все ее обобщенные координаты равны нулю. Это положение системы будем называть начальным положением и обозначать буквой M ₀.

Потенциальная энергия консервативной системы в ее произвольном положении M равна работе действующих на систему сил при перемещении системы из этого произвольного положения M в начальное положение M ₀, то есть

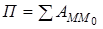. (2.2)

Основные приемы вычисления работы постоянной силы тяжести и упругой силы указаны в прил. 3.

Потенциальная энергия П системы, определяемая по формуле (2.2), зависит только от положения системы, то есть от ее обобщенных координат . Поэтому П всегда может быть представлена в форме

. (2 3)

Для этого достаточно все перемещения, входящие в , выразить через изменения обобщенных координат, используя геометрические соотношения расчетной схемы.

Определение потенциальной энергии для консервативной системы рекомендуется производить в такой последовательности:

· изобразить систему в произвольном положении M, определяемом координатами , производя отсчет координат от начального положения M ₀ системы;

· показать все действующие на систему активные силы;

· отметить перемещение точек приложения сил при переходе системы из положения M ₀ в положение M;

· записать , пользуясь формулами прил. 3;

· выразить все перемещения в через изменения обобщенных координат системы и по формуле (2.2) определить потенциальную энергию системы.

Определим потенциальную энергию системы на рис. 1.3, взяв за обобщенные координаты величины j и s (рис. 2.1).

Начальное положение системы M ₀ возьмем в положении ее статического равновесия, когда j = 0, s = 0; деформация пружины в этом положении системы равна l. В произвольном положении M системы j > 0, s > 0.

Активные силы системы: 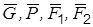; сила упругости (cм. подразд. 1.3).

При перемещении системы из M ₀ в M точка приложения сил 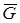и переместится из положения D ₀ в положение D. Точка приложения силы P переместится из положения E ₀ в положение E. Точка A приложения силы F ₂ – неподвижна.

Определим работу сил при перемещении системы из M ₀ в M:

;

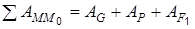где

, , .

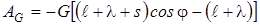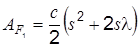Учитывая, что , по формуле (2.2) определим

.

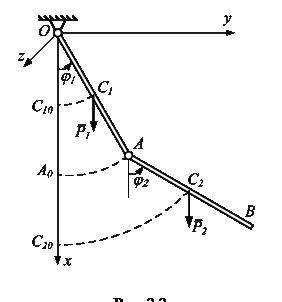
Далее определим потенциальную энергию двойного физического маятника из двух шарнирно связанных стержней ОА и АВ (рис. 2.2) весом Р и длиной 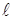каждый. Стержень ОА вращается вокруг горизонтальной оси z, а стержень АВ совершает плоскопараллельное движение в вертикальной плоскости xy.

Система на рис. 2.2 имеет две степени свободы (см. подразд. 1.2). В качестве обобщенных координат возьмем углы j₁ и j₂ – отклонения стержней в произвольном положении М системы от направления оси x. В начальном положении М ₀ системы j₁ = 0 и j₂ = 0.

Активными силами системы являются силы тяжести стержней Р ₁ и Р ₂. При переходе системы из положения М_о в положение М точки приложения сил Р ₁ и Р ₂ опишут криволинейные траектории С ₁₀ С ₁ и С ₂₀ С ₂ соответст­венно. Определим сумму работ сил Р ₁ и Р ₂ при перемещении системы из М в М ₀

.

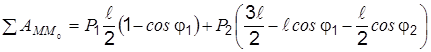Затем по формуле (2.2) имеем

.

2.4. Составление дифференциальных уравнений
движения консервативных систем

Чтобы получить искомые уравнения для консервативной системы, нужно вначале записать функцию Лагранжа L = T – П, затем подставить L в уравнения (2.1). При дифференцировании функции L следует принять во внимание все замечания, относящиеся к дифференцированию функций T в подразд. 1.6.

Далее предлагается самостоятельно сформировать функцию Лагранжа L для системы на рис. 2.1, подставить эту функцию в уравнение Лагранжа (2.1) и убедиться, что полученные этим способом дифференциальные уравнения движения совпадают с уравнениями для той же системы из подразд. 1.6 (пример 1.12).

При решении задач в некоторых случаях может получиться, что одна какая-либо обобщенная координата q_i системы не входит явно в функцию Лагранжа L. Тогда будем иметь . Соответствующее этой координате уравнение Лагранжа в (2.1) имеет вид

.

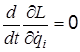Из этого следует, что

. (2.4)

Выражение (2.4) называют циклическим интегралом, а координату q_i – циклической координатой. Наличие циклического интеграла существенно упрощает решение задачи.

2.5. Методика решения задач с помощью уравнений
Лагранжа для консервативных систем

· Проверить, действительно ли консервативна рассматриваемая система (подразд. 2.2).

· Определить число степеней свободы системы и выбрать ее обобщенные координаты (подразд. 1.2 и 1.3).

· Записать выражение кинетической энергии системы в обобщенных координатах (подразд. 1.5).

· Составить выражение потенциальной энергии системы (подразд. 2.3).

· Составить дифференциальные уравнения движения системы (подразд. 2.4).

· Решая полученную систему дифференциальных уравнений, определить искомые величины.

При решении задач надо учитывать замечания, сделанные в подразд. 1.1.

Задача 2.1. Система на рис. 2.3 состоит из призмы A весом 2 P и соединенного с ней шарниром тонкого однородного стержня AB весом P и длиной . При движении системы стержень колеблется в вертикальной плоскости, призма A движется вдоль оси x. Пренебрегая сопротивлением движению, составить дифференциальные уравнения движения этой системы и затем найти зависимость между скоростью призмы и угловой скоростью стержня, если в начальный момент .

Активные силы – силы тяжести призмы и стержня. Поэтому согласно подразд. 2.2 система консервативна.

Система на рис. 2.3 имеет две степени свободы, так как для ее остановки нужно закрепить сначала призму, движущуюся прямолинейно, а затем стержень, вращающийся вокруг оси A.

Положение статического равновесия системы обозначим M ₀, в этом положении стержень вертикален (рис. 2.4).

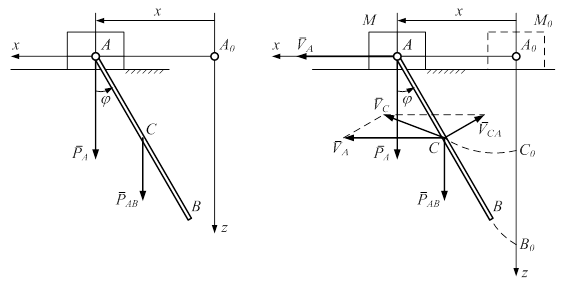
Рис. 2.3 Рис. 2.4

В качестве обобщенных координат возьмем величины x и j. Эти координаты в положении M ₀ равны нулю.

Определим кинетическую энергию системы T = T_A + T_AB.

По формулам (2) и (4) прил. 2

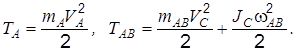
Выразим V_A, w _AB и V_C через обобщенные скорост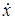и и 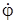: из анализа рис. 2.4 следует, что 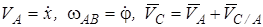, где 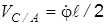; далее по формуле, определяющей диагональ параллелограмма, находим

.

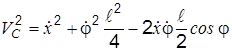Подставляя эти результаты в T и учитывая, что

,

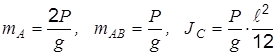получим

.

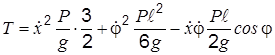Определим потенциальную энергию системы на рис. 2.4. Для этого вычислим работу сил на перемещении системы из положения M в положение M ₀:

.

Далее согласно формуле (2.2) имеем

.

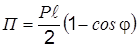Для составления дифференциальных уравнений движения системы вначале найдем функцию Лагранжа

.

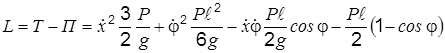Обобщенная координата x не входит явно в L: она является циклической. Ей соответствует циклический интеграл (2.4): или

. (а)

Это первое дифференциальное уравнение движения рассматриваемой системы. Из уравнения (а) при начальных условиях t = 0 , 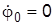получим

.

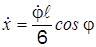Это искомая зависимость между скоростью призмы и угловой скоростью стержня.

Для получения второго дифференциального уравнения движения системы найдем

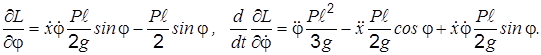
Подставляя эти результаты в (2.1), получим

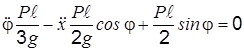. (б)

Уравнения (а) и (б) являются искомыми дифференциальными уравнениями движения рассматриваемой системы.

Далее предлагается самостоятельно решить задачи 2.2 и 2.3.

Задача 2.2. Блок D подвешен к нижнему концу вертикальной пружины, верхний конец которой неподвижен (рис. 2.5). Коэффициент жесткости пружины равен с. Через блок перекинута нерастяжимая нить с грузами А и В на концах, массы грузов соответственно равны m ₁ и m ₂. Выбирая за обобщенные координаты удлинение x пружины из положения статического равновесия и расстояние y груза А от оси блока, составить дифференциальные уравнения движения данной системы. Массой нити и блока пренебречь.

Ответ: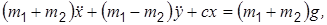

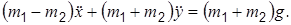
Задача 2.3. Составить дифференциальные уравнения движения системы на рис. 2.2, учитывая условия задачи, соответствующие этому рисунку (см. подразд. 2.3). Сопротивлением движению системы пренебречь. В качестве обобщенных координат взять углы j₁ и j₂.

Ответ:

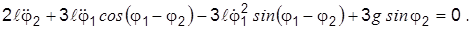
*) Связи системы называются голономными, если их уравнения могут быть записаны в виде, не содержащем производные от координат по времени или дифференциалов координат.

**) Связи системы называются стационарными, если ограничения, накладываемые ими на положение тел и точек системы, не изменяются при движении.

Дата добавления: 2014-12-07