Свойства равномерного распределения

1. С помощью линейного преобразования распределение, равномерное в интервале , сводится к распределению, равномерному в интервале .

2. Если случайная величина имеет непрерывную функцию распределения , то случайная величина имеет равномерное распределение в интервале . Это обстоятельство широко используется в имитационном (статистическом) моделировании.

3. Равномерное распределение является частным случаем обобщенного бета-распределения.

4. Пусть 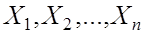– независимые случайные величины, имеющие одну и ту же непрерывную функцию распределения. Тогда распределение дробной части их суммы сходится к равномерному на интервале распределению.

5. С ростом числа слагаемых распределение случайной величины быстро сходится к стандартному нормальному распределению. (Здесь 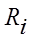– случайная величина, равномерно распределенная на интервале , ).

6. Пусть случайные величины и 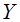имеют абсолютно непрерывное совместное распределение. Тогда при 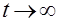распределение дробной части случайной величины 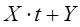сходится к равномерному на интервале распределению.

Пример. Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А.

Решение. Ошибку округления отсчета можно рассматривать как случайную величину , которая распределена равномерно в интервале между двумя соседними целыми делениями. Плотность равномерного распределения , где – длина интервала, в котором заключены возможные значения ; вне этого интервала . В рассматриваемой задаче длина интервала, в котором заключены возможные значения , равна 0,1, поэтому . Легко сообразить, что ошибка отсчета превысит 0,02, если она будет заключена в интервале (0,02, 0,08).

По формуле , получим

.

Дата добавления: 2014-12-07