Свойства - распределения

1. Если – независимые стандартные нормальные случайные величины, то случайная величина имеет 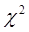-распределение с степенями свободы.

2. 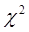-распределение с степенями свободы совпадает с гамма-распределением с параметром масштаба и параметром формы .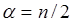

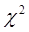3. Случайная величина , имеющая - распределение с степенями свободы, и случайная величина , имеющая гамма-распределение с параметром масштаба 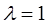и параметром формы , связаны соотношением ~ .

4. Сумма независимых случайных величин , имеющих 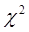-распределение с степенями свободы соответственно имеет 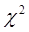-распределение с 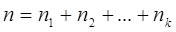степенями свободы.

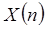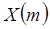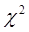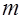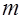5. Независимые случайные величины и , имеющие -распределение с и степенями свободы, соответственно связаны со случайной величиной , имеющей -распределение Фишера-Снедекора с и степенями свободы, соотношением ~ .

6. Случайная величина 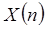имеет такое же распределение, как и случайная величина , то есть ~ .

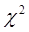7. Случайная величина , имеющая -распределение с степенями свободы, связана со случайной величиной 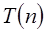, имеющей распределение Стьюдента с степенями свободы, и независимой от 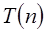стандартной нормальной случайной величиной следующим соотношением ~ .

8. При четном случайная величина связана со случайной величиной , распределенной по закону Пуассона с параметром , соотношением .

Этому соотношению эквивалентны соотношения

, , целое;

, .

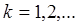Здесь – интеграл вероятностей 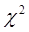-распределения; – функция распределения Пуассона с параметром ; .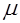

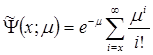9. При случайная величина сходится к стандартному нормальному распределению. Однако эта сходимость довольно медленная. Гораздо быстрее сходится к стандартному нормальному распределению случайная величина .

Распределение 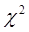нашло широкое применение при проверке статистических гипотез о виде распределения случайной величины 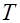, а также в теории надежности – при определении доверительных границ [9].

Распределение хи-квадрат может быть определено как сумма квадратов 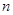-независимых случайных величин с нулевым средним значением и единичным средним квадратическим отклонением. На рис. 7 показаны формы кривых распределения.

Значения квантилей 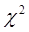-распределения представлены в приложении 3, заимствованные из.

Пример. При испытаниях системы электроавтоматики распределение отказов по интервалам наработки представлены в табл. 8. Определить по критерию согласия 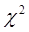принадлежность совокупности данного распределения отказов экспоненциальному закону с параметром и достоверностью .

Таблица 3

Интервал наработок до отказа, ч	5-10	10-20	20-30	30-40	40-45	45-50
Число отказов в интервале

Для расчета квантили 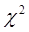-распределения составим дополнительную табл.4.

Здесь – длина интервала.

Так как предполагаемый теоретический закон распределения наработки до отказа экспоненциальный, он имеет один параметр. Тогда число степеней свободы равно разности между числом интервалов и числом параметров распределения, то есть .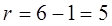

Таблица 4

Интервал наработок до отказа, ч	5-10	10-20	20-30	30-40	40-45	45-50	Примечание
Число отказов в интервале
Функция отказов (теоретическая)	0,98	0,999	0,999	0,999	0,98	0,98
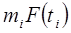
	9,8	7,999	5,994	5,994	4,9	4,9
	0,004	0,000001	0,000006	0,000006	0,002	0,002	Сумма 0,008

При достоверности и числе степеней свободы по таблице приложения 3 находим квантиль: .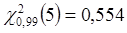

Полученное значение .

Это свидетельствует о том, что гипотеза 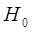о принадлежности статистического распределения теоретическому (экспоненциальному) подтверждается с вероятностью 0,99.

Ответ: статистические данные подтверждают экспоненциальный закон распределения наработки до отказа.

Дата добавления: 2014-12-07