
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейная регрессия. Коррелированность и зависимость случайных величин
|
|
|
|
Коррелированность и зависимость случайных величин
Две случайные величины  и
и 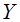 называют коррелированными, если их корреляционный момент (коэффициент корреляции) отличен от нуля;
называют коррелированными, если их корреляционный момент (коэффициент корреляции) отличен от нуля;  и
и 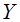 называют некоррелированными величинами, если их корреляционный момент равен нулю.
называют некоррелированными величинами, если их корреляционный момент равен нулю.
Две коррелированные величины также и зависимы.
Рассмотрим двумерную случайную величину 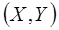 , где
, где  и
и 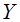 – зависимые случайные величины. Представим одну из величин, как функцию другой. Ограничимся приближенным представлением величины
– зависимые случайные величины. Представим одну из величин, как функцию другой. Ограничимся приближенным представлением величины 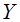 в виде линейной функции величины
в виде линейной функции величины  [5]:
[5]:
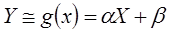 ,
,
где 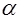 и
и 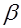 – параметры, подлежащие определению. Это можно сделать различными способами: наиболее распространенный из них – метод наименьших квадратов.
– параметры, подлежащие определению. Это можно сделать различными способами: наиболее распространенный из них – метод наименьших квадратов.
Функцию  называют «наилучшим приближением»
называют «наилучшим приближением» 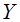 , в смысле метода наименьших квадратов, если математическое ожидание
, в смысле метода наименьших квадратов, если математическое ожидание 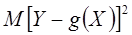 принимает наименьшее возможное значение; функцию
принимает наименьшее возможное значение; функцию 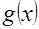 называют среднеквадратической регрессией
называют среднеквадратической регрессией 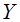 на
на  .
.
Теорема. Линейная средняя квадратическая регрессия 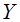 на
на  имеет вид
имеет вид
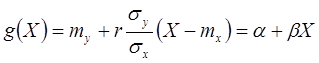 ,
,
где 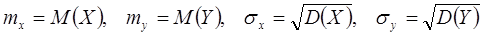 ;
; 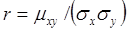 – коэффициент корреляции величин
– коэффициент корреляции величин  и
и 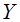 .
.
Коэффициент 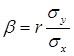 называют коэффициентом регрессии
называют коэффициентом регрессии 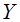 на
на  , а прямую:
, а прямую: 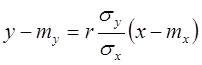 , (8)
, (8)
называют прямой среднеквадратической регрессии 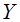 на
на  .
.
Минимальное значение функции 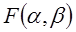 равно
равно 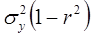 . Величину
. Величину 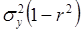 называют остаточной дисперсией случайной величины
называют остаточной дисперсией случайной величины 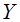 относительно случайной величины
относительно случайной величины  ; она характеризует величину ошибки, которую допускают при замене
; она характеризует величину ошибки, которую допускают при замене 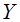 линейной функцией
линейной функцией 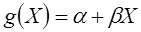 . При
. При 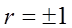 остаточная дисперсия равна нулю; другими словами, при этих крайних значениях коэффициента корреляции не возникает ошибки при представлении
остаточная дисперсия равна нулю; другими словами, при этих крайних значениях коэффициента корреляции не возникает ошибки при представлении 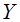 , в виде линейной функции от
, в виде линейной функции от  .
.
Итак, если коэффициент корреляции 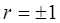 , то
, то 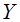 и
и  связаны линейной функциональной зависимостью.
связаны линейной функциональной зависимостью.
Аналогично можно получить прямую среднеквадратической регрессии  на
на 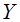 :
: 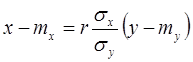 (9)
(9)
(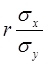 – коэффициент регрессии
– коэффициент регрессии  на
на 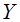 ) и остаточную дисперсию
) и остаточную дисперсию 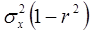 величины
величины  относительно
относительно 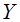 .
.
Если 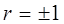 , то обе прямые регрессии, как видно из (7) и (8), совпадают. Из уравнений (7) и (8) следует, что обе прямые регрессии проходят через точку
, то обе прямые регрессии, как видно из (7) и (8), совпадают. Из уравнений (7) и (8) следует, что обе прямые регрессии проходят через точку 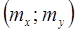 , которую называют центром совместного распределения величин
, которую называют центром совместного распределения величин  и
и 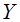 .
.
Вопросы для самопроверки по разделу 1
1. Как выглядит график плотности равномерного распределения?
2. Как выглядит график функции равномерного распределения?
3. Что такое нормальный закон распределения?
4. Как называется и как выглядит график плотности нормального распределения?
5. Как выглядит график 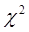 -распределения?
-распределения?
6. Какое распределение называется распределением Стьюдента?
7. Какое распределение называется распределением Фишера-Снедекора?
8. Какое распределение называется показательным распределением?
9. Какое распределение называется распределением Эрланга?
10. Что определяет функцию надежности?
11. Что называют законом распределения дискретной двумерной случайной величины?
12. Как определяется функция распределения двумерной случайной величины?
13. Какова геометрическая интерпретация функции распределения двумерной случайной величины?
14. Какими свойствами обладают функции двумерной случайной величины?
15. Чему равна вероятность попадания случайной точки в полуполосу?
16. Чему равна вероятность попадания случайной точки в прямоугольник?
17. Что называется плотностью совместного распределения вероятностей двумерной непрерывной случайной величины?
18. Какую поверхность называют поверхностью распределения?
19. Какими свойствами обладает двумерная плотность вероятности?
20. Как связана плотность совместного распределения и функция распределения двумерной случайной величины?
21. Что называется условным распределением?
22. Что называется условной плотностью?
23. Что называют условным математическим ожиданием?
24. Что такое функция регрессии?
25. Что называется корреляционным моментом двух случайных величин?
26. Чему равен корреляционный момент двух независимых случайных величин?
27. Когда две случайные величины называются некоррелированными?
28. Как вычисляется коэффициент регрессии?
29. Каким уравнением определяется прямая среднеквадратической регрессии?
Раздел 2. Элементы математической статистики
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1003; Нарушение авторских прав?; Мы поможем в написании вашей работы!