Теоретические основы. (набирается в редакторе WORD и сдается на дискете при сдаче зачета

Отчет

(набирается в редакторе WORD и сдается на дискете при сдаче зачета. Отчет должен быть не менее двух стандартных страниц шрифт 14 New Roman, поля по 1,5 см с каждой стороны, интервал между строками 1,5 и состоять из следующих разделов:

· Название (например: Изучение курса акций РАО ЕС за октябрь-ноябрь 2003г. ФИО выполнявших студентов полностью

· Исходные данные по акциям в виде таблицы

· Краткий анализ хозяйственной деятельности компании (берется из задания№1)

· Эконометрическое обоснование выбора уравнений Делается на основе заданий 1-4 и включает все основные пункты обоснования:

1. выбор уравнения,

2. проверка его значимости,

3. остатки и их анализ с помощью теоремы Гаусса-Маркова

1. исследования остатков на нормальность

Для получения зачета нужно:

· выполнит задания №№1-5.

· В электронном виде сдать отчет.

· исправить все замеченные преподавателем неточности.

· Принести зачетную книжку.

ГЛАВА 5. СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений. Различают несколько видов систем уравнений:

Ø Система независимых уравнений - когда каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х:

Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов;

Ø Система рекурсивных уравнений - когда зависимая переменная у одного уравнения выступает в виде факторах в другом уравнении:

Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов;

Ø Система взаимосвязанных (совместных) уравнений - когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других - в правую:

Такая система уравнений называется структурной формой модели.

Эндогенные переменные - взаимозависимые переменные, которые определяются внутри модели (системы) у.

Экзогенные переменные - независимые переменные, которые определяются вне системы х.

Предопределенные переменные - экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы.

Коэффициенты а и b при переменных - структурные коэффициенты модели.

Система линейных функций эндогенных переменных от всех предопределенных переменных системы - приведенная форма модели:

где 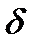- коэффициенты приведенной формы модели.

Идентификация – это единственность соответствия между приведенной и структурной формами модели.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

1) идентифицируемые;

2) неидентифицируемые;

3) сверхидентифицируемые.

Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.

Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.

Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Если обозначить число эндогенных переменных в -м уравнении системы через 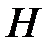, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение, — через , то условие идентифицируемости модели может быть записано в виде следующего счетного правила:

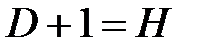
	уравнение идентифицируемо
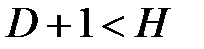
	уравнение неидентифицируемо
	уравнение сверхидентифицируемо

Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.

Если необходимое условие выполнено, то далее проверяется достаточное условие идентификации.

Достаточное условие идентификации. Уравнение идентифицируемо, если определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.

Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:

1) косвенный метод наименьших квадратов;

2) двухшаговый метод наименьших квадратов;

3) трехшаговый метод наименьших квадратов;

4) метод максимального правдоподобия с полной информацией;

5) метод максимального правдоподобия при ограниченной информации.

Рассмотрим вкратце сущность каждого из этих методов.

Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы.

1. Структурная модель преобразовывается в приведенную форму модели.

2. Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты .

3. Коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК).

Основная идея ДМНК – на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.

Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название ДМНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.

Сверхидентифицируемая структурная модель может быть двух типов:

1) все уравнения системы сверхидентифицируемы;

2) система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений

Дата добавления: 2014-12-07