Пример 2. Изучается модель вида

Изучается модель вида

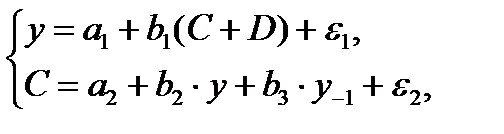
где у - валовой национальный доход;

y_-1 - валовой национальный доход предшествующего года;

С - личное потребление;

D - конечный спрос (помимо личного потребления);

ε₁ и ε₂ - случайные составляющие.

Информация за девять лет о приростах всех показателей дана в табл. 3.1.

Таблица 5.1

Год	D	y-1	у	С	Год	D	y-1	у	С
	-6,8	46,1	3,1	7,4		44,7	17,8	37,2	8,6
	22,4	3,1	22,8	30,4		23,1	37,2	35,7	30,0
	-17,3	22,8	7,8	1,3		51,2	35,7	46,6	31,4
	12,0	7,8	21,4	8,7		32,3	46,6	56,0	39,1
	5,9	21,4	17,8	25,8	Σ	167,5	239,1	248,4	182,7

Для данной модели была получена система приведенных уравнений:

Требуется:

1. Провести идентификацию модели.

2. Рассчитать параметры первого уравнения структурной модели.

Решение:

1. В данной модели две эндогенные переменные (у и С) и две экзогенные переменные (D и y_-1). Второе уравнение точно идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1 + 1.

Первое уравнение сверхидентифицировано, так как в нем на параметры при С и D наложено ограничение: они должны быть равны. В этом уравнении содержится одна эндогенная переменная у. Переменная С в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с переменной D. В данном уравнении отсутствует одна экзогенная переменная, имеющаяся в системе. По счетному правилу идентификации получаем: 1 + 1 = 2: D + 1 > Н. Это больше, чем число эндогенных переменных в данном уравнении, следовательно, система сверх-идентифицирована.

2. Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.

Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной С. Для этого в приведенное уравнение

С = 8,636 + 0,3384 ∙ D + 0,2020 ∙ y_-1

подставим значения D и y_-1, имеющиеся в условии задачи. Получим:

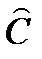₁ = 15,8; ₂ = 16,8; ₃ = 7,4; ₄ = 14,3; ₅ = 15,0; ₆ = 27,4;

₇ = 24,0; ₈ = 33,2; ₉ = 29,0.

Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения С на теоретические и рассчитываем новую переменную С + D (табл. 3.2).

Таблица 5.2

Год	D		+ D	Год	D		+ D
	-6,8	15,8	9,0		44,7	27,4	72,1
	22,4	16,8	39,2		23,1	24,0	47,1
	-17,3	7,4	-9,9		51,2	33,2	84,4
	12,0	14,3	26,3		32,3	29,0	61,3
	5,9	15,0	20,9	Σ	167,5	182,9	350,4

Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную

+ D через Z. Решаем уравнение

y = a₁ + b₁ ∙ Z.

Система нормальных уравнений составит:

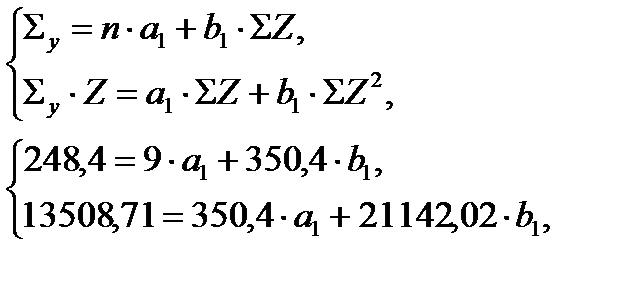
а₁ = 7,678; b₁ = 0,512.

Итак, первое уравнение структурной модели будет таким:

У = 7,678 + 0,512 ∙ (С + D).

Дата добавления: 2014-12-07