Решение. Решение типовых задач

Решение типовых задач

Пример 1

Требуется:

1. Оценить следующую структурную модель на идентификацию:

2. Исходя из приведенной формы модели уравнений

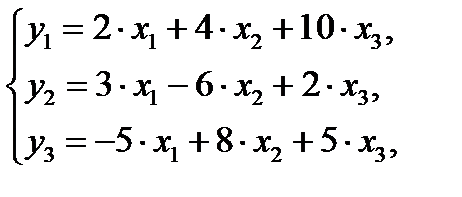
найти структурные коэффициенты модели.

1. Модель имеет три эндогенные (у₁, у₂, у_з) и три экзогенные (х₁, х₂, х₃) переменные.

Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации.

Первое уравнение.

Н: эндогенных переменных - 2 (у ₁ у₃),

отсутствующих экзогенных - 1 (х₂).

Выполняется необходимое равенство: 2 =1 + 1, следовательно, уравнение точно идентифицируемо.

Д: в первом уравнении отсутствуют у₂ и х₂ - Построим матрицу из коэффициентов при них в других уравнениях системы:

Уравнение	Отсутствующие переменные
	y2	х2
Второе	-1	а22
Третье	b32

Det А = -1 ∙ 0 – b₃₂ ∙a₂₂ ≠ 0.

Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.

Второе уравнение.

Н: эндогенных переменных - 3 (у₁, у₂, у_з)_,

отсутствующих экзогенных - 2 (х₁,x₃)

Выполняется необходимое равенство: 3 = 2 + 1, следовательно, уравнение точно идентифицируемо.

Д: во втором уравнении отсутствуют xi и х₃. Построим матрицу из коэффициентов при них в других уравнениях системы:

Уравнение	Отсутствующие переменные
x1	x з
Первое	а11	а13
Третье	а31	а33

Det А = а₁₁ ∙ а₃₃ - а₃₁ ∙ а₁₃ ≠ 0.

Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо.

Третье уравнение.

Н: эндогенных переменных - 2 (у₂, у₃),

отсутствующих экзогенных - 1 (х ₂).

Выполняется необходимое равенство: 2=1 + 1, следовательно, уравнение точно идентифицируемо.

Д: в третьем уравнении отсутствуют у₁ и х₂. Построим матрицу из коэффициентов при них в других уравнениях системы:

Уравнение	Отсутствующие переменные
у1	x2
Первое	-1
Второе	b21	а22

DetA = -l a₂₂ - b_2l 0 ≠ 0.

Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо.

Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов.

2. Вычислим структурные коэффициенты модели:

1) из третьего уравнения приведенной формы выразим х₂ (так как его нет в первом уравнении структурной формы):

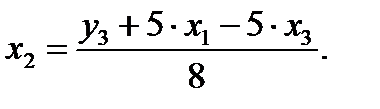
Данное выражение содержит переменные у_з, х₁ и х₃, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение х₂ в первое уравнение приведенной формы модели (ПФМ):

2) во втором уравнении СФМ нет переменных х₁ и х₃. Структурные параметры второго уравнения СФМ можно будет определить в два этапа:

Первый этап: выразим х₁ в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения:

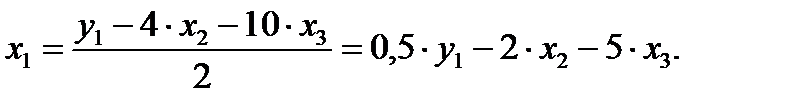
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует х₃, которого нет в СФМ.

Выразим х₃ из третьего уравнения ПФМ:

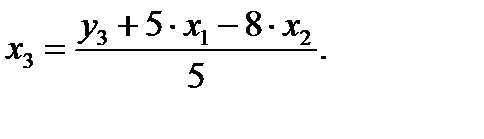
Подставим его в выражение х₁:

Второй этап: аналогично, чтобы выразить х₃ через искомые у₁, у₃ и х₂, заменим в выражении х_з значение х₁ на полученное из первого уравнения ПФМ:

Следовательно,

x₃ = 0,033 ∙ у₃ + 0,083 ∙ у₁ – 0,6 ∙ x₂.

Подставим полученные х₁ и х_з во второе уравнение ПФМ:

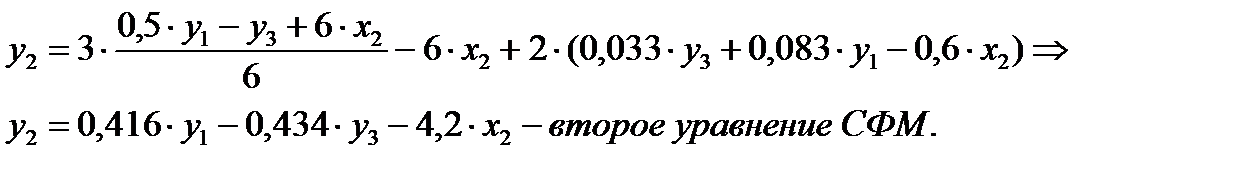
Это уравнение можно получить из ПФМ иным путем. Суммируя все уравнения, получим

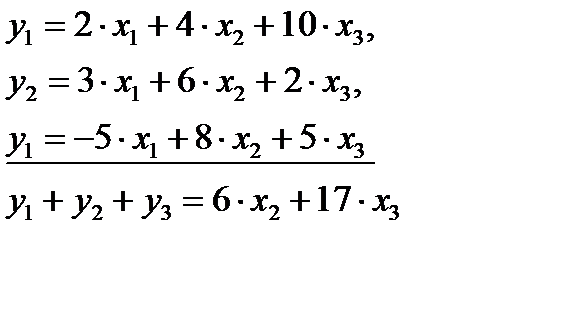
Далее из первого и второго уравнений ПФМ исключим х₁ домножив первое уравнение на 3, а второе - на (-2) и просуммировав их:

Затем аналогичным путем из полученных уравнений исключаем х₃, а именно:

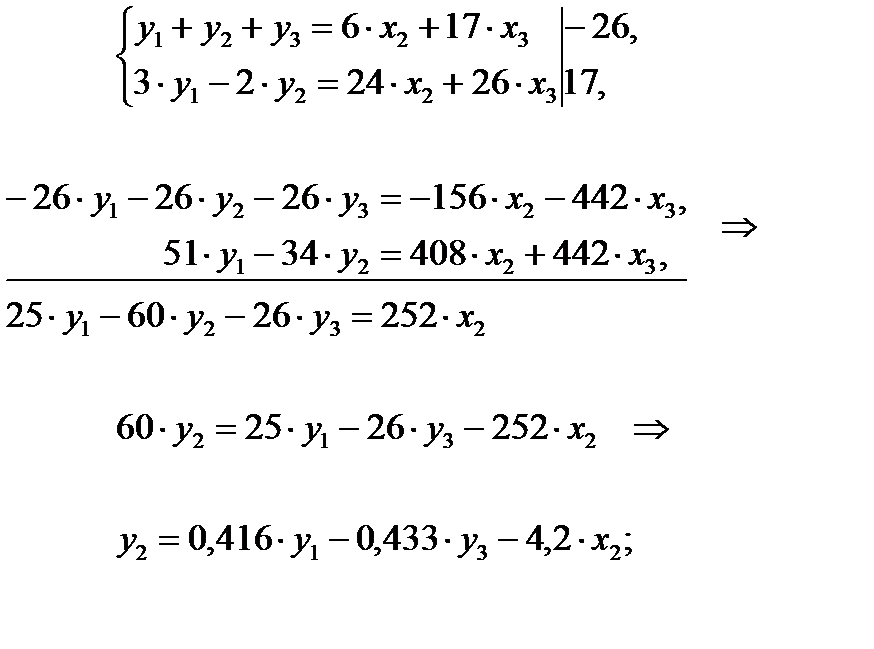
3) из второго уравнения ПФМ выразим х₂, так как его нет в третьем уравнении СФМ:

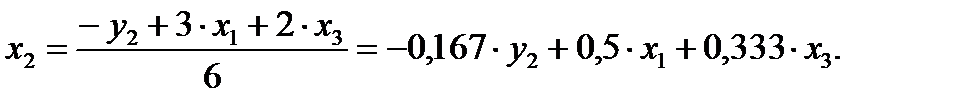
Подставим полученное выражение в третье уравнение ПФМ:

Таким образом, СФМ примет вид

Дата добавления: 2014-12-07