Пример 3. Таблица 5.3 Год Годовое потребление свинины на душу населения, фунтов, y1 Оптовая цена за фунт

Имеются данные за 1990-1994 гг. (табл. 3.3).

Таблица 5.3

Год	Годовое потребление свинины на душу населения, фунтов, y1	Оптовая цена за фунт, долл., у2	Доход на душу населения, ДОЛЛ., x1	Расходы по обработке мяса, % к цене, x2
		5,0
		4,0
		4,2
		5,0
		3,8

Требуется:

Построить модель вида

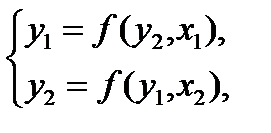
рассчитав соответствующие структурные коэффициенты.

Решение:

Система одновременных уравнений с двумя эндогенными и двумя экзогенными переменными имеет вид

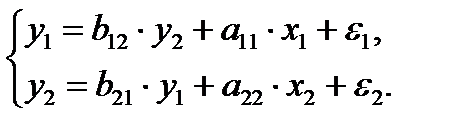
В каждом уравнении две эндогенные и одна отсутствующая экзогенная переменная из имеющихся в системе. Для каждого уравнения данной системы действует счетное правило 2 = 1 + 1. Это означает, что каждое уравнение и система в целом идентифицированы.

Для определения параметров такой системы применяется косвенный метод наименьших квадратов.

С этой целью структурная форма модели преобразуется в приведенную форму:

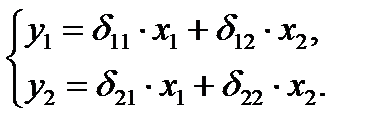
в которой коэффициенты при х определяются методом наименьших квадратов.

Для нахождения значений δ₁₁ и δ₁₂ запишем систему нормальных уравнений:

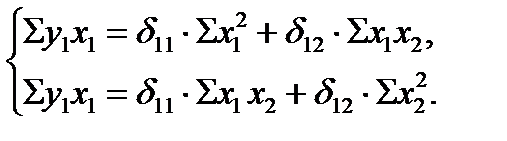
При ее решении предполагается, что х и у выражены через отклонения от средних уровней, т. е. матрица исходных данных составит:

	y1	y2	x1	x2
	-3	0,6	-200
	-1	-0,4	-200	-1
		-0,2		-1
	-1	0,6
		-0,6		-7
Σ		0,0

Применительно к ней необходимые суммы оказываются следующими:

Σу₁х₁ = 1600; Σу₁х₂ = -37; Σx²₁ = 180 000;

Σx₁х₂ = - 1900; Σx²₂ = 96.

Система нормальных уравнений составит:

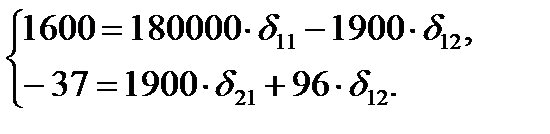
Решая ее, получим:

δ₁₁ = 0,00609; δ₁₂ = -0,26481.

Итак, имеем y₁ =0,00609 • x₁ - 0,26481 • х₂.

Аналогично строим систему нормальных уравнений для определения коэффициентов δ₂₁ и δ₂₂:

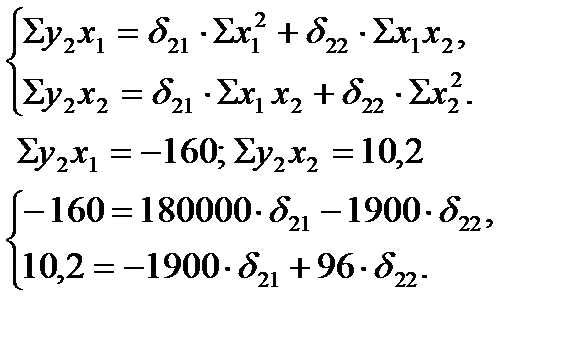
Следовательно,

δ₂₁ =0,00029; δ₂₂ =0,11207,

тогда второе уравнение примет вид

y₂ = 0,00029 • x₁ + 0,11207 • х₂.

Приведенная форма модели имеет вид

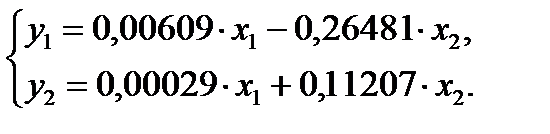
Из приведенной формы модели определяем коэффициенты структурной модели:

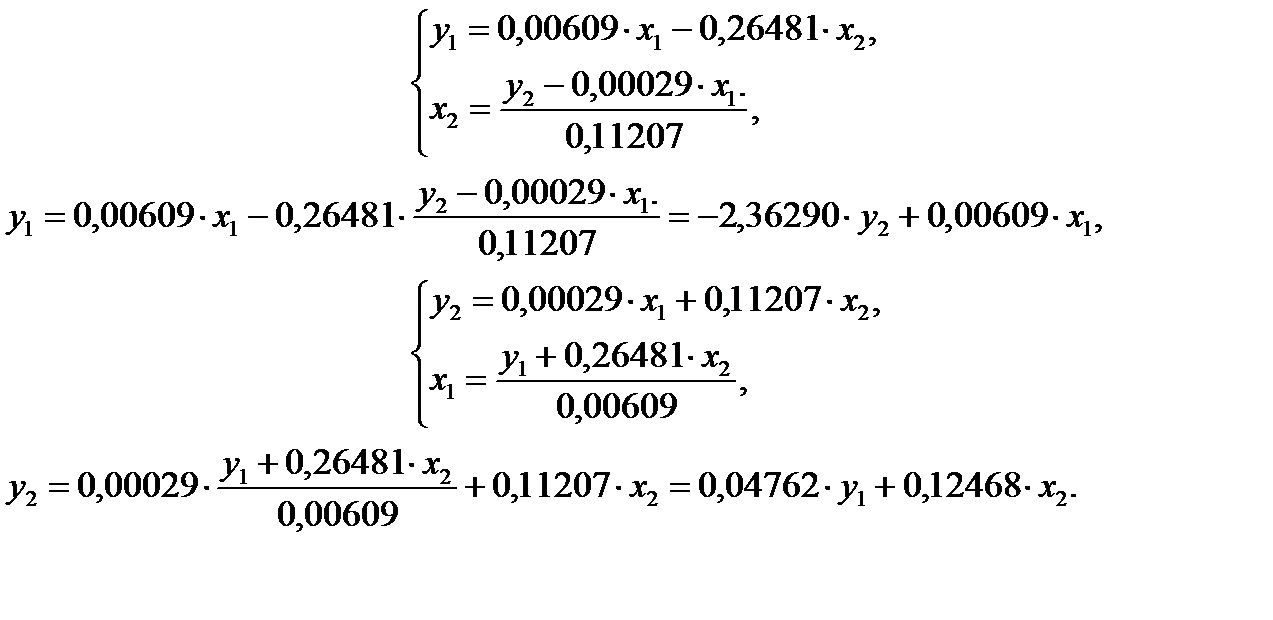
Итак, структурная форма модели имеет вид

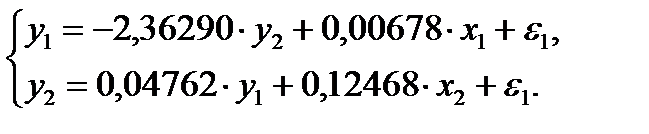
Дата добавления: 2014-12-07