Аналитическая геометрия

Задача 1. Написать разложение вектора 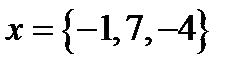по векторам , ,

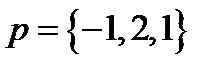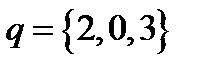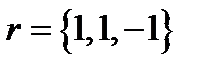
Решение:

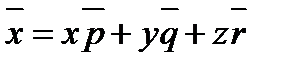или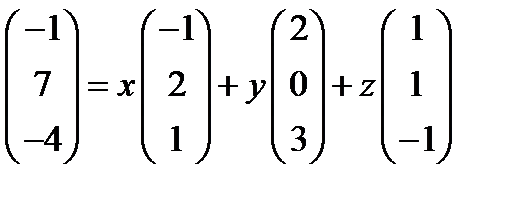

отсюда

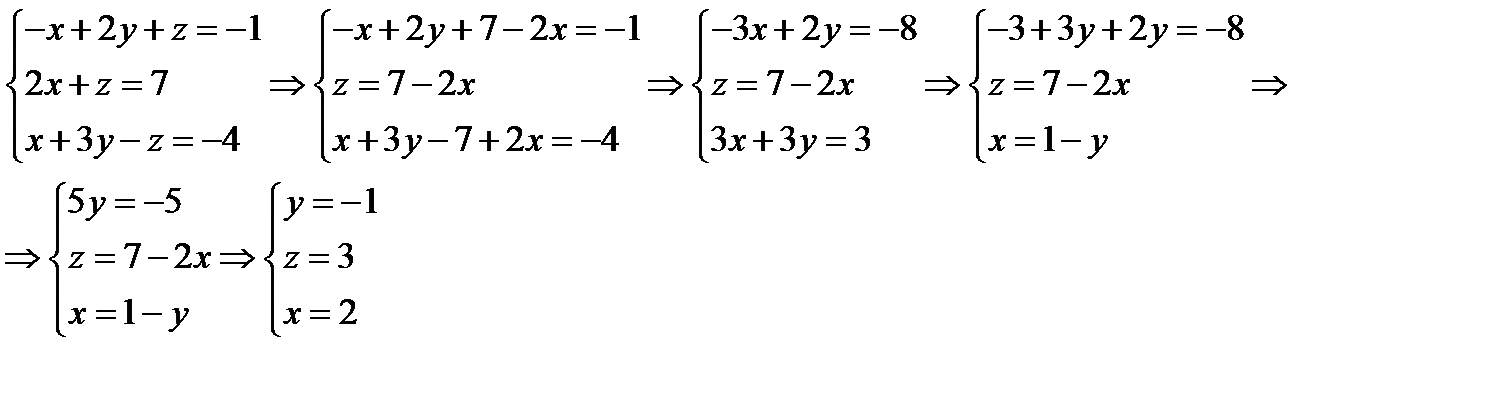
таким образом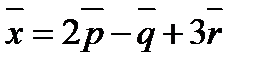

Задача 2. Коллинеарны ли векторы 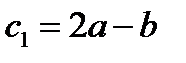и 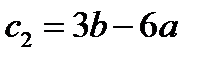, построенные по векторам ,

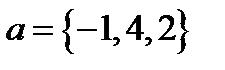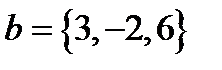
Решение:

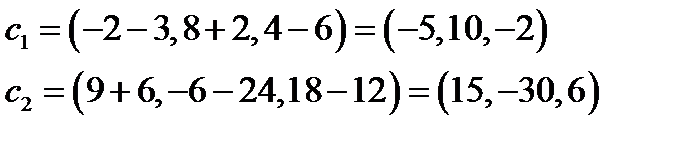
Координаты векторов 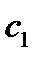и 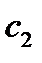пропорциональны, т.е. 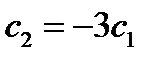, а значит векторы 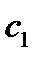и 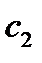коллинеарны.

Задача 3. Найти косинус угла между векторам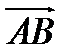и и . , ,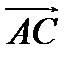

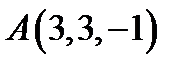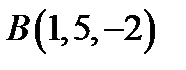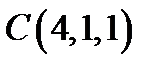
Решение:

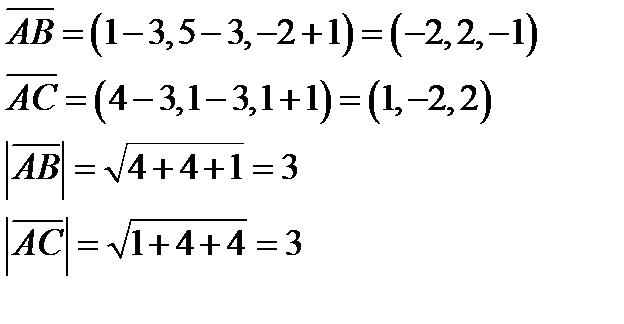
Скалярное произведение векторов равно:

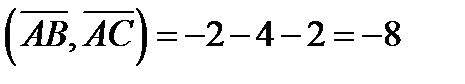
Находим косинус угла между векторам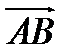и и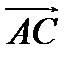

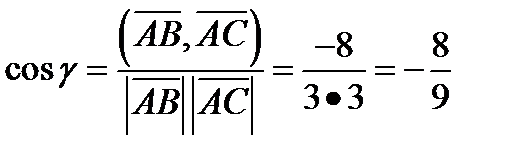
Задача 4. Вычислить площадь параллелограмма, построенного на векторах a и b. , , , ,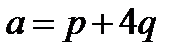

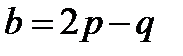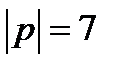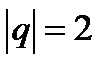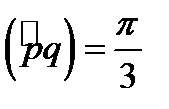
Решение:

Найдем векторное произведение

так как 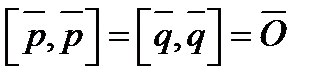и , то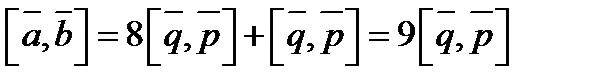

Площадь параллелограмма, построенного на векторах a и b, будет равна

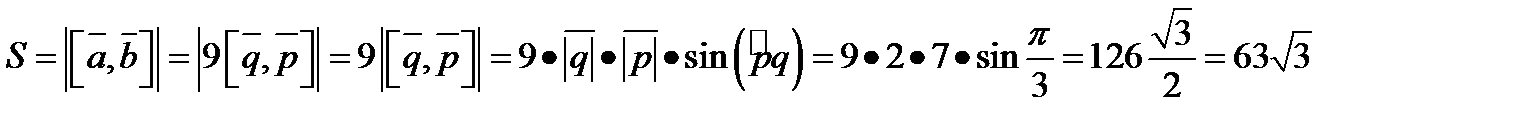
Задача 5. Компланарны ли векторы , ,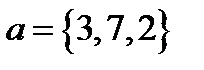

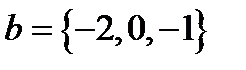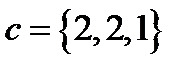
Решение:

Найдём смешанное произведение векторов

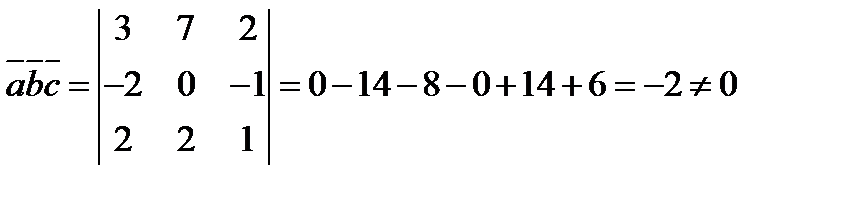
Следовательно векторы не компланарны

Задача 6. Вычислить объем тетраэдра с вершинами в точках 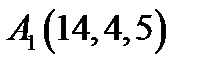, , 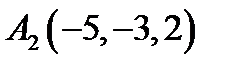, 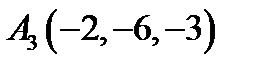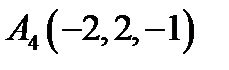и его высоту, опущенную из вершины 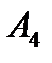на грань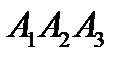

Решение:

объём тетраэдра равен

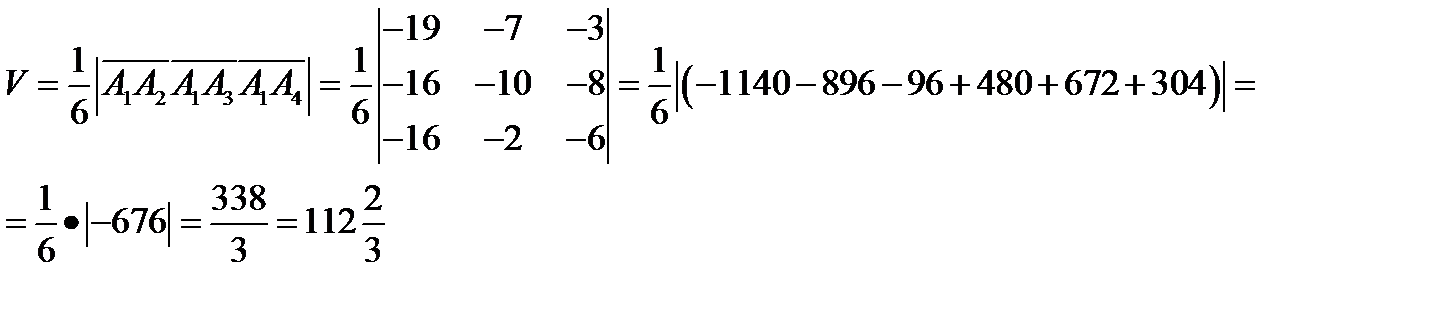
Объем тетраэдра также вычисляется по формул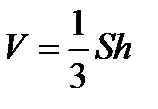е , где 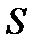– площадь грани 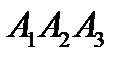, 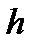– высота, опущенная из вершины 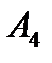на грань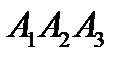

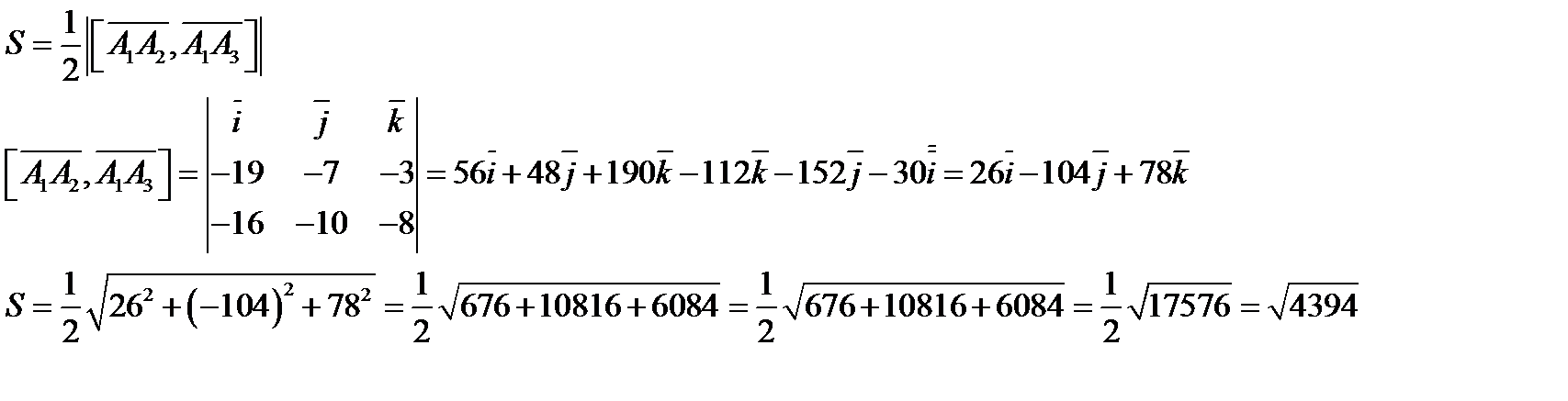следовательно, высота будет равна

Задача 7. Найти расстояние от точки 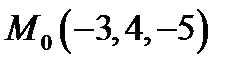до плоскости, проходящей через точки , ,

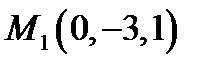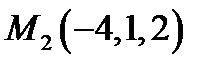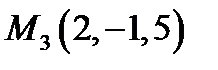
Решение:

Уравнение плоскости будет иметь вид

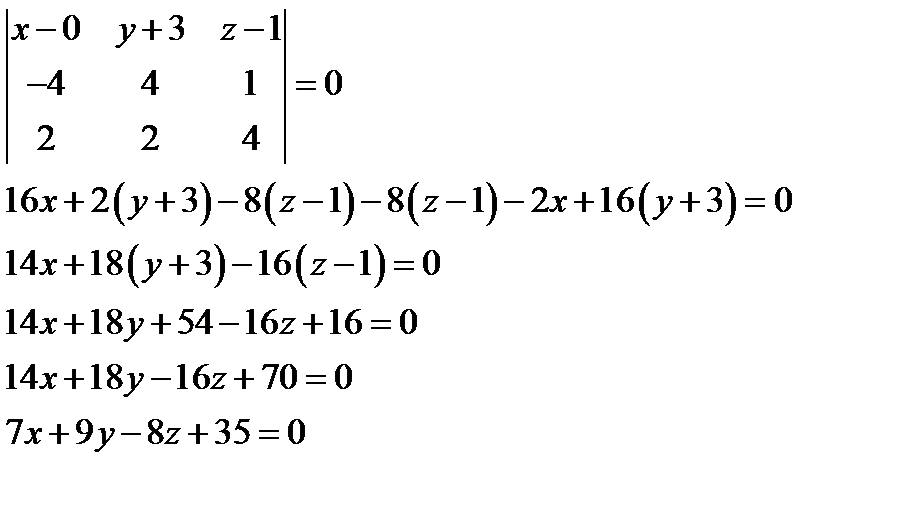
Расстояние от точки 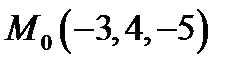до плоскости будет равно

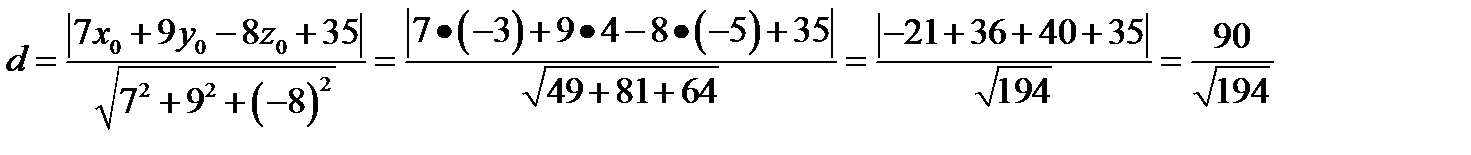
Задача 8. Написать уравнение плоскости, проходящей через точку 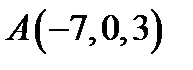перпендикулярно вектору . ,

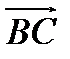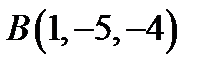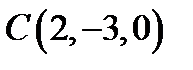
Решение:

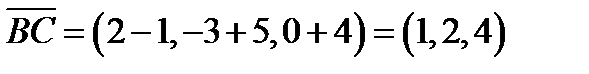
уравнение плоскости, проходящей через точку 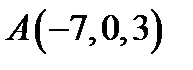перпендикулярно вектору 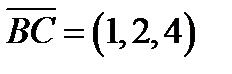будет иметь вид:

Задача 9. Найти угол между плоскостями ,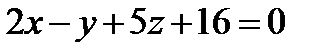

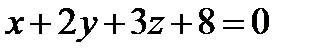
Решение:

Нормальные векторы плоскосте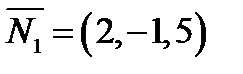й:

и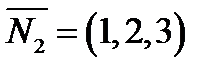

Найдем угол между плоскостями

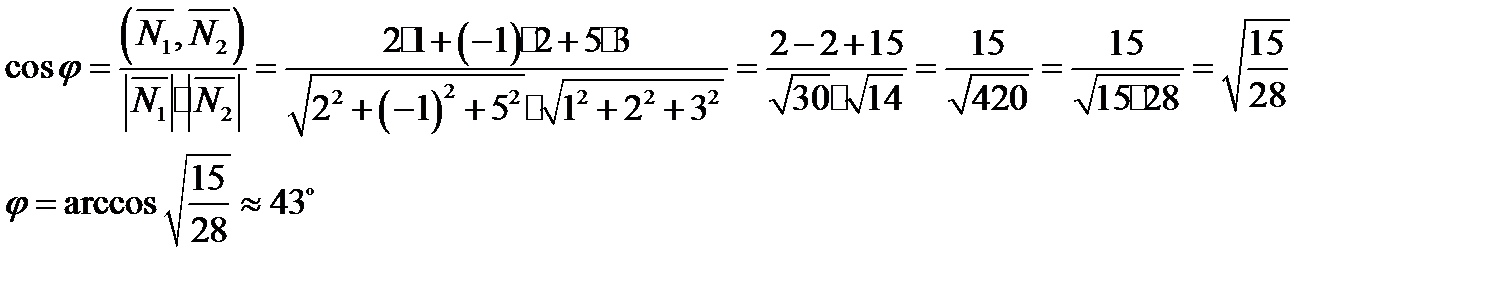
Задача 10. Найти координаты точки 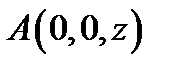, равноудаленной от точек 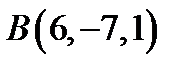и

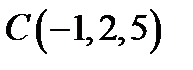
Решение:

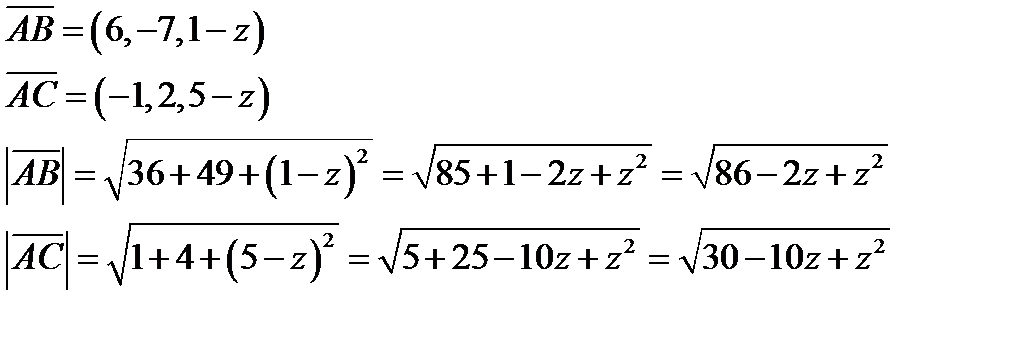
по условию задачи 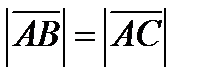, значит

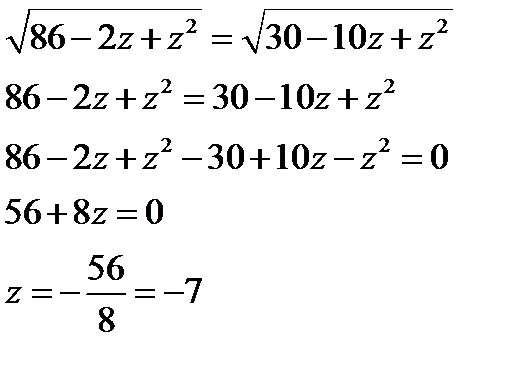
Таким образом, координаты точки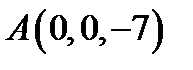

Задача 12. Написать канонические уравнения прямой ,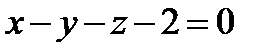

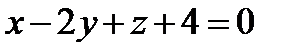
Решение:

Каноническое уравнение прямой имеет вид 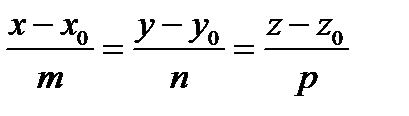, где 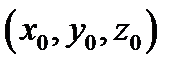– координаты какой-либо точки прямой, 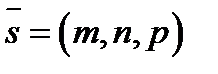– направляющий вектор.

Нормальные вектора плоскосте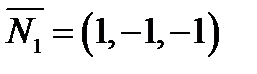й: и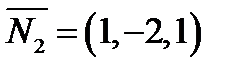

Находим направляющий вектор

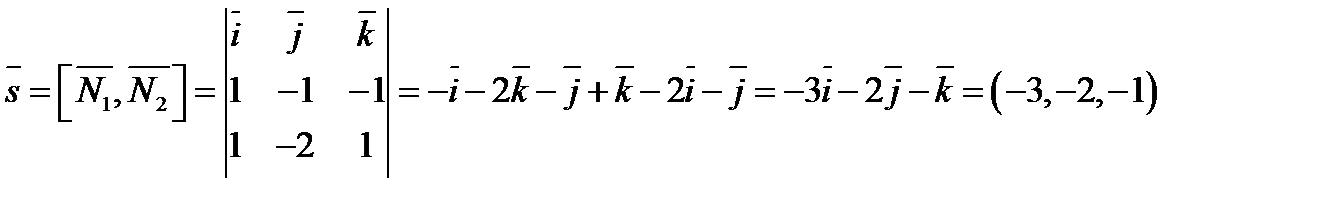
Находим какую-нибудь точку прямой. Пусть 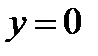, тогда

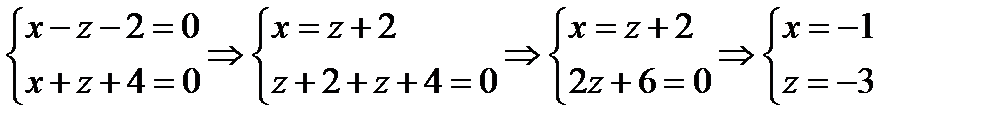
Получаем каноническое уравнение прямой

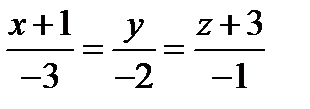
Задача 13. Найти точку пересечения прямой и плоскости. ,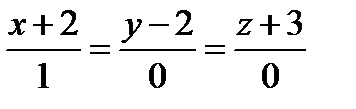

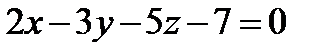
Решение:

Запишем параметрические уравнения прямой:

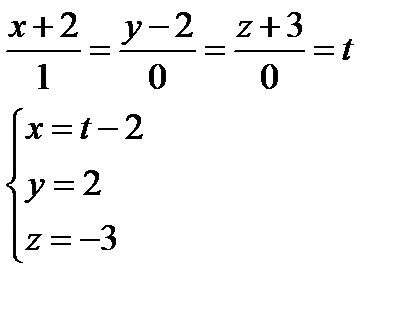
Подставим в уравнение плоскости

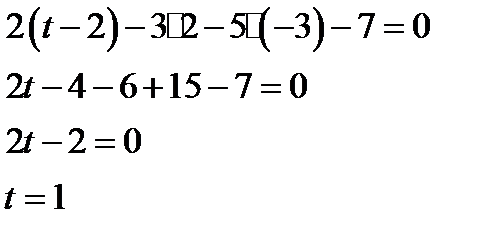
Найдем координаты точки пересечения прямой и плоскости

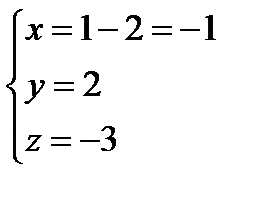
Получаем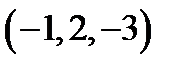

Дата добавления: 2014-12-27