Контрольная работа № 4. Построить на плоскости ХОУ область интегрирования , вычислить по

Задача 211-220.

Построить на плоскости ХОУ область интегрирования, вычислить по

области (D),ограниченной заданными линиями.

211. у=2х у=о х=1

212. у=х у=4-х х=0

213. у= у=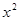4

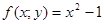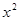214. у= у=4

215. 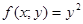у=3х у=3 х=0

216. у= 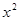у=0 х=2

217. у= 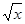у=2 х=0

218. у=2-х у=0 х=0

219. у= 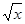у=0 х=4

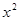220. у= у=

Задача 221-230.

Даны криволинейный интеграл и три точки на плоскости ХОУ:

О(0;0), А(2;0), В(2;4).Вычислить данный интеграл от точки О до точки В по трем различным контурам:

1)по ломанной прямой АОВ,

2) по отрезку прямой ОВ,

3) по дуге параболы у=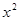

Полученные результаты сравнить и объяснить их совпадение или несовпадения.

221. 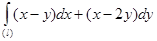226.

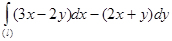
222. 227.

223. 228.

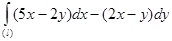
224. 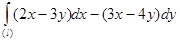229.

225. 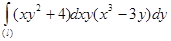230.

Задача 231-240.

1) Комплексное число z изобразить вектором на комплексной плоскости и записать в тригонометрической и показательной формах,

2) решить предложенное уравнение

221. z=2+2i

222.

223.

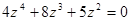
224.

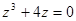
225.

226.

227.

228.

229.

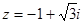
230.

Задача 231-240.

Дано дифференциальное уравнение первого порядка. Найти общее решение и частное решение, удовлетворяющее заданному начальному условию.

231. у(1)=1

232.

234. у(1)=2

235.

236.

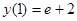
237. у(1)=3

238. у(1)=2

239.

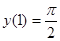
240.

Задача 241-250.

Даны дифференциальное уравнение второго порядка, допускающее понижение порядка.

Найти частное решение, удовлетворяющее заданному начальному условию.

241.

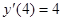
242.

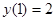
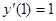
243.

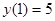
244.

245.

246.

247.

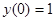
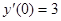
248.

249.

250.

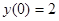
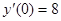
Задача 251-260.

Даны линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Найти общее решение.

251. 256.

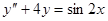
252. 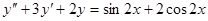257.

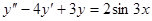
253. 258.

254. 259.

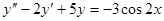
255. 256.

Задача 261-270.

Даны линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.Применяя операционный метод, найти частное решение этих уравнений, удовлетворяющее указанным начальным условиям.

261.

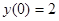
262.

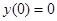
263.

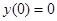
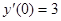
264.

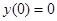
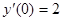
265.

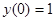
266.

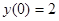
267.

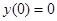
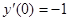
268.

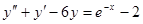
269.

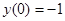
270.

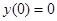
Дата добавления: 2014-12-27