Метод узловых потенциалов

Если в схеме имеется узлов меньше, чем ветвей, то целесообразно применить для определения токов метод узловых потенциалов. 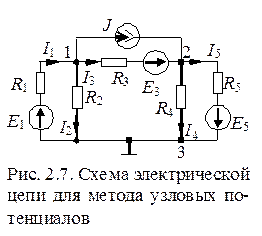В этом методе будет выполняться второй закон Кирхгофа, поэтому для расчета цепи необходимо будет составить уравнений на единицу меньше, чем узлов в схеме.

На рис. 2.7 приведена схема, содержащая 6 ветвей и 3 узла. По первому закону Кирхгофа составим уравнения для первого и второго узлов:

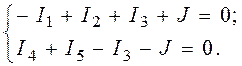(2.10)

Выразим каждый ток через потенциалы на концах ветвей, используя закон Ома или второе уравнение Кирхгофа:

С учетом того, что потенциал определяется с точностью до постоянной составляющей, примем потенциал одного из узлов равным нулю (например, φ ₃=0). Подставим в уравнения (2.10) вместо сопротивлений проводимости ветвей g_k =1/ R_k, а вместо напряжений – разность потенциалов U ₁₂= φ ₁– φ ₂; U ₁₃= φ ₁–0; U ₂₃= φ ₂. Тогда уравнения (2.10) будут иметь вид

после преобразования получим

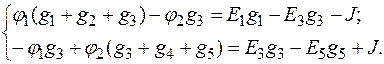
(2.11)

где g ₁₁= g₁ + g ₂+ g ₃ и g ₂₂= g ₃+ g ₄+ g ₅ – суммы проводимостей ветвей, сходящихся соответственно в первом и втором узлах; g ₁₂ – проводимость ветви между первым и вторым узлом; J _{1 пр} = E ₁ g ₁– E ₃ g ₃– J и J _{2 пр} = E ₃ g ₃- E ₅ g ₅+J –приведенные токи для первого и второго узла.

При этом слагаемые E_кg_к и J_к оказываются всегда с плюсом, когда источники направлены к соответствующему узлу, слагаемые φ_kg_kk – всегда положительны, а слагаемые φ_kg_kn – всегда отрицательны.

Если в схеме будет 4 узла, то система уравнений по методу контурных токов будет иметь вид

(2.12)

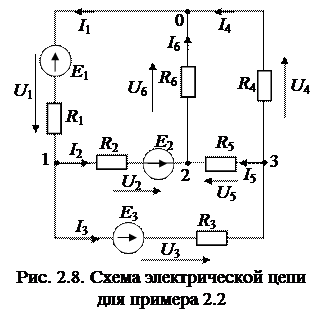
П р и м е р 2.2. На рис. 2.8 изображена электрическая схема с шестью неизвестными токами. ЭДС источников Е ₁=6 В, Е ₂ =12 В и Е ₃ =18 В; сопротивления ветвей r ₁= r ₂= r ₃=2 Ом и r ₄ = r ₅= = r ₆=6 Ом. Пользуясь методом узловых потенциалов, определить токи во всех ветвях.

Р е ш е н и е. Пусть потенциал точки О равен нулю. Запишем уравнения для узлов с потенциалами φ ₁, φ ₂, φ ₃:

(g ₁+ g ₂ + g ₃) φ ₁– g ₂ φ ₂– g ₃ φ ₃ = – E ₁ g ₁– E ₂ g ₂– E ₃ g ₃;

– g ₂ φ ₁+(g ₂+ g ₅ + g ₆) φ ₂– g ₂ φ ₂– g ₅ φ ₃ = – E ₂ g ₂;

– g ₃ φ ₁ – g ₅ φ ₂+(g ₃+ g ₄ + g ₅) φ ₃ = – E ₃ g ₃.

После подстановки числовых значений проводимостей и ЭДС получим

Решая совместно эти уравнения, определяем искомые потенциалы: φ ₁ = –3 В; φ ₂ = 9 В; φ ₃ = 18 В. Для определения токов в ветвях следует зададимся их положительными направлениями. При выбранных положительных направлениях токов (рис. 2.8)

I ₁= (φ ₀– φ ₁– E ₁) g ₁ =4,5 А; I ₂= (φ ₁– φ ₂+ E ₂) g ₂ =0 А;

I ₃= (φ ₁– φ ₃+ E ₃) g ₃ =0 А; I ₄= (φ ₃– φ ₀) g ₄ =3 А;

I ₅= (φ ₃– φ ₂) g ₅ =1,5 А; I ₆= (φ ₂– φ ₀) g ₆ = –0,5 А.

Дата добавления: 2014-12-27