Свойства линейных электрических цепей

Линейные электрические цепи имеют несколько свойств, которые формируются в виде отдельных принципов. На их основе возможны преобразования и расчеты цепей.

Принцип наложения (суперпозиции). Для линейных цепей в соответствии с уравнением (2.3) ток в k -ветви равен сумме токов, вызываемых каждой из ЭДС схемы в отдельности. Это позволяет рассчитывать параметры электрических цепей методом наложения – сначала определить все токи от одной ЭДС, затем от другой и т.д., а потом все составляющие токов от разных ЭДС сложить. Отметим, что мощности от частичных токов суммировать нельзя – в баланс мощностей должны входить полные токи.

П р и м е р 2.6. Для схемы рис. 2.14, а определить токи, если R ₁=2 Ом, R ₂=4 Ом; R ₃=6 Ом, J =5 А, Е =20 В.

Р е ш е н и е. 1. Задаем положительное направление токов (рис. 2.14, а).

2.Методом наложения определяем токи в ветвях сначала от источника тока (рис. 2.14, б)

затем от источника ЭДС (рис. 2.14, в)

,

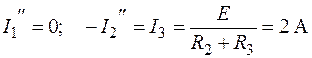затем суммируем частичные токи и определяем истинные значения токов в ветвях

3.Составляем баланс мощностей

P_n = I ₁² R ₁+ I ₂² R ₂+ I ₃² R ₃=150 Вт,

P_и = EI ₁+ J (I ₁ R ₁+ I ₂ R ₂)=150 Вт, P_n=P_и.

Принцип взаимности. Для линейной цепи ток в k -ветви I_k, вызванный источником E_m, находящимся в m -ветви, равен току I_m в m -ветви, если источник E_m перенести в k -ветвь, т.е. I_k=E_mg_km=E_mg_mk. При использовании принципа взаимности при расчете необходимо следить за взаимным соответствием направлений токов и ЭДС в ветвях.

П р и м е р 2.7. В схеме рис. 2.15 при нахождении ключей в положении 1 включен только источник ЭДС Е₁=10 В. При этом известны только I ₂=1 А, I ₃=3 А. Определить ток I ₁, если все ключи определяются в положении 2, когда включены Е ₂=20 В, Е ₃=30 В.

Р е ш е н и е. 1. Используя принцип взаимности, определяем частичную составляющую тока I ₁′ от ЭДС, находящейся во второй ветви и равной E ₂=20 В, 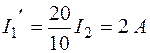. Аналогично, частичная составляющая тока I ₁" от ЭДС, находящейся в третьей ветви I ₁"=30/10 I ₃=9 A.

2. Используя принцип наложения, определяем полный ток в первой ветви I ₁= I ₁'+ I ₂"=2+9=11 A.

Принцип компенсации. В любой электрической цепи без изменений токораспределения можно заменить сопротивление источником ЭДС, значение которого равно падению напряжения на сопротивлении и направлена встречно току на этом сопротивлении. Аналогичную замену можно сделать и источником тока J, значение которого равно току в этом сопротивлении и направлена на ту же сторону. Это следует из второго и соответственно первого законов Кирхгофа при переносе слагаемого из левой части уравнения в правую.

П р и м е р 2.8. В схеме (рис. 2.16, а) Е ₁=5 В, R ₁=1 Ом, R ₂=2 Ом, R ₃=1 Ом. Заменить R ₃ источником ЭДС и тока.

Р е ш е н и е. 1. Определим токи в схеме рис.2.16, а

2. Заменяем R ₃ источником ЭДС (рис. 2.16, б)

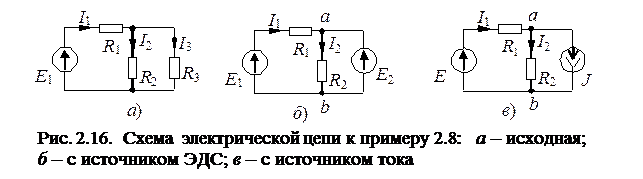
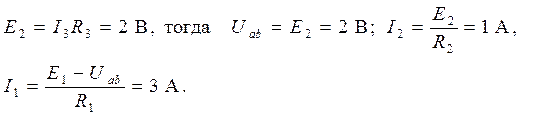
3. Заменим ток I ₃ источником тока J=I ₃=2 А (рис. 2.16, в), тогда

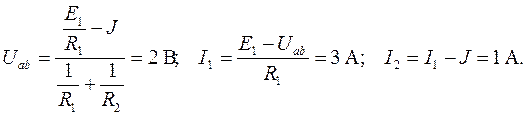
Принцип линейности. Если в линейной электрической цепи изменяется ЭДС или сопротивление в какой-либо одной цепи, то две любые значения (U или I) двух любых ветвей связаны друг с другом линейными зависимостями вида

y=a+bx (2.14)

т.е. U=a+bI или U ₁= c+dU ₂ или I ₁= k+mI ₂.

Аналогичная зависимость получается при изменениях этих величин в двух ветвях, тогда

y=a+bx+cz. (2.15)

Коэффициенты а, b в уравнении (2.14) определяются экспериментально или расчетным путем. Для этого необходимо знать значения напряжений (или токов) для двух различных режимов. Подставляя эти значения в уравнение 2.14, получим систему двух уравнений с двумя неизвестными. Решая систему уравнений, определим коэффициенты а, b.

Аналогично, для определения коэффициентов а, b, c в уравнении 2.15 необходимо иметь данные для трех режимов и решить систему из трех уравнений. Отметим, что в качестве у, x, z могут использоваться только U и I, но ни в коем случае ни R.

П р и м е р 2.9. В схеме рис. 2.17 при первом положении переключателя (холостой ход) I _1хх=1 А, I _2хх=5 А, при втором положении (короткое замыкание) I _1r=2 А, I _2к=4 А. Определить ток I ₁, если при третьем положении переключателя I ₂=4,5 А.

Р е ш е н и е. Подставляем значения токов I ₁ и I ₂ для двух режимов в уравнения вида (2.14)

Решая систему уравнений, определяем а =6, b = –1, т.е. между токами существует зависимость I ₁=6– I ₂. При токе I ₂ = 4,5 А, ток

I ₁=6–4,5=1,5 А.

Теорема вариаций. Изменение тока одной ветви, вызванное приращением сопротивления в другой ветви, определяется уравнением , (2.16)

где g ₁₂ –взаимная проводимость первой и второй ветвей; Δ R – приращение сопротивления во второй ветви; I ₂, g ₂₂ – ток и входная проводимость второй ветви.

На рис. 2.18, а приведена схема, в которой во второй ветви увеличилось сопротивление на Δ R. Токи также изменились. По принципу компенсации заменим Δ R на Δ Е (рис. 2.18, б), где Δ Е =Δ R (I ₂+Δ I ₂). На основании принципа наложения можно считать, что Δ I ₁ и Δ I ₂ вызваны Δ Е, т.е.

Δ I ₁= –Δ Eg ₁₂= – g ₁₂(I ₂+Δ I ₂)Δ R, Δ I ₂= –Δ Еg ₂₂= – g ₂₂(I ₂+Δ I ₂)Δ R.

Отсюда . (2.17)

П р и м е р 2.10. В схеме на рис. 2.18 g ₁₂=3/26 См, g₂₂=5/26 См, а токи I ₁=7 А, I ₂=3 А. Определить I ₁ и I ₂, при изменении сопротивления Δ R =1 Ом.

Р е ш е н и е. По уравнению 2.17 определяем Δ I ₁= –0,29 А, ΔI₂ = 0,483 А. Тогда токи I ₁=6,71 А, I ₂=2,517 А.

Дата добавления: 2014-12-27