Метод контурных токов

Передаточные коэффициенты

После решения системы уравнений, составленной по законам Кирхгофа, токи в ветвях можно записать следующим образом:

I ₁ = g ₁₁ E ₁+ g ₁₂ Е ₂+…+ h ₁₁ J ₁+ h ₁₂ J ₂+…

I ₂ = g ₂₁ E ₁+ g ₂₂ E ₂+…+ h ₂₁ J ₁+ h ₂₂ J ₂+… (2.3)

где E_n – ЭДС ветви n, а J_к – источники токов, подключенные к узлу k.

Коэффициенты g_mm (т.е. с одинаковыми индексами – g ₁₁, g ₂₂, g ₃₃…) называют входными (или собственными) проводимостями. Они равны току соответствующей ветви, когда в этой ветви включена ЭДС, равная 1 В, т.е. E_m =1, а в остальных ветвях ЭДС нет.

Величина, обратная входной проводимости, называется входным сопротивлением

R_вx=R_mm= 1 /g_mm.

Коэффициенты с разными индексами g_mn называют взаимными проводимостями (или передаточными). Взаимная проводимость g_mn равна току в ветви m при действии единственной ЭДС, равной 1 В и включенной в ветви n, когда в остальных ветвях отсутствуют ЭДС и источники токов.

Взаимные проводимости можно определять опытным путем. Для этого из исследуемой цепи удаляют все источники ЭДС и источники токов, кроме одной ЭДС в необходимой ветви E_k. Измерив токи I_k и I_m, рассчитывают взаимную проводимость g_mk=I_m/E_k и входную проводимость g_kk=I_k/E_k.

Безразмерные коэффициенты h_mk называют передаточными коэффициентами. Они численно равны току в ветви m при единственном источнике тока J_к = 1 А, подключенному к узлу k.

Можно уменьшить число уравнений для расчета токов в разветвленной цепи, если составлять уравнения так, чтобы первый закон Кирхгофа выполнялся автоматически. При этом число уравнений будет равно числу независимых контуров, т.е. числу уравнений, составляемых по второму закону Кирхгофа.

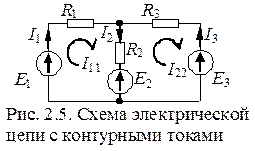Ток в любой ветви электрической схемы можно представить в виде суммы нескольких токов, каждый их которых замыкается по своему контуру, оставаясь вдоль него неизменным. Такие составляющие действительных токов называют контурными токами. На рис. 2.5 действительный ток I ₂ можно представить как разность контурных токов I ₁₁ и I ₂₂, т.е.

I ₂= I ₁₁– I ₂₂. (2.4)

При этом уравнение по второму закону Кирхгофа, составленное для 1-го контура, имеет вид I ₁ R ₁+ I ₂ R ₂= E ₁– E ₂. С учетом уравнения (2.4)

I ₁₁ R ₁+(I ₁₁– I ₂₂) R ₂= E ₁– E ₂. (2.5)

Аналогично для другого контура

I ₂ R ₂+ I ₃ R ₃= E ₃– E ₂, (I ₁₁– I ₂₂) R ₂– I ₂₂ R ₃= E ₃– E ₂. (2.6)

Преобразуем уравнения (2.5) и (2.6):

или

I ₁₁ R ₁₁– I ₂₂ R ₁₂= E ₁₁;

– I ₁₁ R ₂₁+ I ₂₂ R ₂₂= E ₂₂,

где R ₁₁ – сумма сопротивлений всех ветвей, входящих в первый контур; R ₁₂ – сопротивление ветви, общей для первого и второго контура; E ₁₁ – сумма всех ЭДС, входящих в первый контур.

Соответствующие ЭДС берутся со знаком «минус», если они направлены против направления обхода контура. Аналогичные значения получаются для второго контура.

Для любого числа контуров

R ₁₁ I ₁₁+ R ₁₂ I ₂₂+ R ₁₃ I ₃₃+…= E ₁₁;

R ₂₁ I ₁₁+ R ₂₂ I ₂₂+ R ₂₃ I ₃₃+…= E ₂₂, (2.7)

или в матричной форме

[ R ][ I ]=[ E ], (2.8)

Слагаемые R ₁₁ I ₁₁, R ₂₂ I ₂₂ всегда положительны, а слагаемые с различными индексами R ₁₂ I ₂₂, R ₁₃ I ₃₃ записывают со знаком «минус», если токи контуров через общее для них сопротивление направлены встречно.

Если в схеме имеются источники токов, то их рассматривают, как ветви с известными токами. Образуя контур с этим известным током J (для этого необходимо выбрать любые ближайшие ветви, через которые замкнется контур), уравнение для этого контура не составляют (так как ток известен), но в уравнениях других контуров появятся слагаемые типа R_knJ_n со знаком минус, если контурный ток смежного контура направлен встречно току источника тока J_n. На рис. 2.6 приведена схема с источником тока.

Образуя контур с источником тока J, включающий ветвь с сопротивлением R ₄, будем считать известным контурный ток J. Два других контурных тока I ₁₁ и I ₂₂ определим, решая систему уравнений

(2.9)

Отметим, что в последнее уравнение вошло слагаемое R ₄ J, так как через сопротивление R₄ протекают в одном направлении контурные токи I ₂₂ и J.

Зная контурные токи, можно определить действительные токи как сумму или разность контурных токов. Для рис. 2.6

I ₁= I ₁₁, I ₂= I ₁₁– I ₂₂, I ₃= I ₂₂, I ₄= I ₂₂+ J.

Дата добавления: 2014-12-27