Конечно-разностные уравнения и тепловые схемы для двумерного и трехмерного распределений температуры

Рассмотрим двумерную пластину толщиной 6, плотностью материала р = p(x1,x2) и удельной теплоемкостью с = c(x1,x2)- Коэффициент теплопроводности пластины λ = λ(x1,x2,t) является функцией координат и времени. Внутри пластины имеется внутренний источник теплоты интенсивностью ф{ x1,x2, t), который зависит от времени и координат вдоль пластины. С обеих поверхностей пластины происходит теплообмен со средой; α' = α'(x1,x2, t)> Т'а = T'a(x1,x2, t) и α" = α"(x1,x2, t). Та'' = Та''(x1,x2,t)- коэффициенты теплоотдачи и температуры среды на верхней и нижней поверхностях пластины соответственно. Пластину будем считать настолько тонкой, чтобы изменением температуры по ее толщине l можно было пренебречь. В этом случае температурное поле пластины является двухмерным и изменяется только по осям x1,x2 и во времени t. Интегральное и дифференциальное уравнения баланса пластины уже были рассмотрены в п. 2.4.2.

Нестационарное двумерное температурное поле пластины описывается уравнением (см. (2.41))

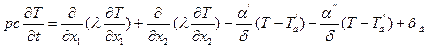
Разобьем пластину плоскостями, параллельными осям х1и х2 (рис. 3.6). Расстояние между плоскостями вдоль оси х1 обозначим Δх1,i, а вдоль оси х2 -Δx2,q. В результате пластина будет представлять собой совокупность непересекающихся прямоугольных параллелепипедов (конечных объемов) размерами Δх1,i * Δx2,q * 6, где i и q - номера параллелепипедов вдоль осей х1и х2 соответственно, так что произвольный параллелепипед будет иметь номер i,q. Площадь поперечного сечения параллелепипеда i,q, перпендикулярного оси х1 обозначим A1,q, а по оси х2 – A2,i,-, причем A1,q = Δx2,q *6, A2,i = Δх1,i*6. Координаты граней i, q-гo параллелепипеда равны х1,i-1/2., х1,i+1/2 - вдоль оси x1 и x2,q-1/2, x2,q+1/2 - вдоль оси x2 (рис. 3.6). В центре каждого параллелепипеда (выделенных объемов Viq) поместим по одному узлу, так что номер параллелепипедa совпадает с номером узла. Координаты узла iq по оси х1 и х2 равны x1,i и X2,q соответственно. Расстояние между узлами i-1,q и iq обозначим h1,i, а между узлами i, q - 1 и iq - h2,q

Рассмотрим баланс теплоты в iq-ом конечном объеме Viq. Согласно интегральному уравнению теплового баланса (2.36) для iq -го конечного элемента справедливо следующее уравнение

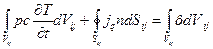(3.23)

где Viq = Δх1,i * Δx2,,q * 6 - объем элемента iq; Siq - площадь поверхности объема Viq.

Поверхностный интеграл в уравнении (3.23) представляет собой полный тепловой поток, пересекающий поверхность объема Viq. Рассмотрим сначала случай, когда внешние поверхности пластины теплоизолированы, а затем рассмотрим пластину с теплообменом ее поверхностей в среду.

3.2.1. Двумерная пластина с теплоизолированными внешними поверхностями. Для пластины с теплоизолированными поверхностями полный тепловой поток, пронизывающий поверхность выделенного объема Viq равен (рис. 3.6)

(3.24)

Получим выражения для тепловых потоков в выражении (3.24).

Тепловой поток Qi-1/2,q, распространяющийся вдоль оси x1 и пересекающий грань выделенного объема, имеющую координату х1,i-1/2, входит через грань контрольного объема площадью A1,q и равен

(3.25)

Где х2,q-координата узлов по оси х2.

Плотность теплового потока q(x1,x2,q), согласно закону Фурье, равна

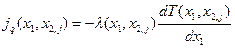
откуда

После интегрирования по х1в пределах от хi-1/2,q до xiq получим

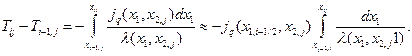
Отсюда, с учетом выражения (3.25), полный тепловой поток вдоль оси x1, пересекающий грань объема Viq с координатой x1,i-1/2 и площадью А1,q равен

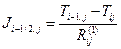
Отсюда, с учетом выражения(3.25)полный тепловой поток вдоль оси х1,пересекоющий грань объёма Viq с координатой х1,i-1/2 и площадью Aiq равен

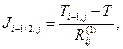(3.26)

Где

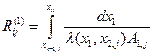(3.27)

кондуктивное тепловое сопротивление вдоль оси х1 между узлами i-1, q и iq.

Аналогично, тепловой поток Qiq-1/2 вдоль оси х2, пересекающий грань контрольного объема площадью A2q равен

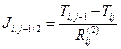(3.28)

где

(3.29)

кондуктивное тепловое сопротивление вдоль оси х2 между узлами i, q - 1 и iq.

Точно также определяются тепловые потоки Qi+1/2,q и Qi,q +1/2, они равны

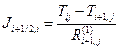и 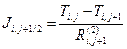(3.30)

где 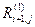, и 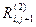- кондуктивные тепловые сопротивления, определяемые по формулам вида (3.27) и (3.29) соответственно.

Для практических расчетов вместо формул (3.27), (3.29) применяют более простые формулы, а именно

где λi-1/2,q = λ (xl,i-1/2,x2,q), λi,q-1/2 = λ (xl,i,x2,q-1/2) - коэффициенты теплопроводности в точках с координатами x1 = xl,i-1/2, х2 = x2,q и х1 = x1,i, х2 = x2,q-1/2 соответственно.

Подставляя тепловые потоки (3.26), (3.28), (3.30) в (3.24), а затем в уравнение баланса (3.23) и приняв, что производная t в первом члене уравнения (3.23) определяется в узле iq получим

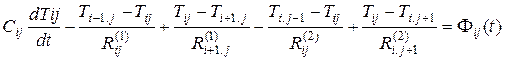(3.31)

Где С_iq - полная теплоёмкость конечного объёма V_iq, Ф_iq(t) – полный тепловой поток внутреннего источника теплоты в конечном объёме V_iq, определяется по соответствующим формулам

, (3.32)

Дата добавления: 2014-12-27