Уравнение баланса теплоты в движущейся жидкости

Уравнение баланса массы

Рассмотрим жидкость плотностью ρ, движущуюся со скоростью v. Уравнение баланса массы или, как его еще называют, уравнение непрерывности получается непосредственно из общего уравнения баланса (2.3) для удельной массы а = М/М = 1, где М - масса жидкости в произвольном неподвижном объеме V. Подставляя плотность потока массы жидкости q_М=ρυ, вытекающую из объема V через ограничивающую ее поверхность S, в уравнения (2.3) при ф=0, получим уравнение баланса массы в интегральной форме

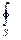= - ρυndS (2.4)

и в дифференциальной форме уравнение непрерывности

div(ρυ)=0. (2.5)

Когда в уравнении (2.5) ρ= const, то получим уравнение непрерывности несжимаемой жидкости

divυ=0. (2.6)

Приведем уравнения баланса теплоты в движущейся жидкости в интегральной и дифференциальной формах. Из этих уравнений, как следствие, получается уравнение теплопроводности в твердом теле. Рассматриваются уравнения для жидкости, движущейся в канале.

2.3.1. Уравнение баланса теплоты в движущейся несжимаемой жидкости. Движение жидкости сопровождается одновременным протеканием разнообразных физических процессов: теплопроводностью; потерей механической энергии в результате внутреннего трения и турбулентного перемешивания, т.е. диссипацией энергии; работой, затрачиваемой на изменение плотности жидкости в результате сжатия или расширения; выделением теплоты от внутренних источников, обусловленных поглощением излучения, прохождением электрического тока, химическими реакциями. Все эти процессы, в конечном итоге, приводят к возникновению теплоты.

Для тепловой энергии Е, Дж, с удельной величиной q, относящейся к единице массы, запишем общее интегральное уравнение баланса

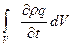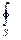= - qdS+ 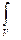фdV, (2.7)

в котором тепловой поток q равен

q= - λgrad T+ ρqυ, (2.8)

а объемная плотность внутреннего источника теплоты в единицу времени ф, Вт/м³ определяется суммой плотностей источника ф_d, обусловленного диссипацией, источника ф_ρ, обусловленного сжатием (расширением) и источника ф_q, обусловленного внутренними источниками теплоты (химическими реакциями, электрическим током, излучением и т.д.), т.е.

ф= ф_d + ф_ρ + ф_q. (2.9)

При этих допущениях дифференциальное уравнение баланса энтальпии примет вид

ρс_р + ρс_рvgradТ= div(λgrad T)+ ф_q. (2.10)

Данное уравнение справедливо и для турбулентного течения несжимаемой жидкости, но для мгновенных значений скорости и температуры.

Дата добавления: 2014-12-27