Сопряженный конвективный теплообмен

Течение жидкости, ограниченной стенками канала, в ряде случаев необхо­димо рассматривать с учетом теплового взаимодействия стенки и потока жид­кости. Совместный анализ процессов теплопередачи в жидкости и в стенке канала с учетом граничных условий на внешней поверхности стенки носит, название сопряженной задачи теплообмена.

2.5.1. Уравнение баланса теплоты жидкости в канале. Уравнение баланса теплоты жидкости (см. (2.10)) для выделенного объема V_f ограничен­ного поверхностью S_f, в интегральной форме имеет вид

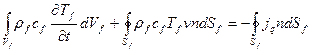, (2.15)

.

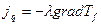Решение этих уравнений приводит к интегральному уравнению

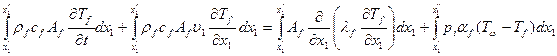, (2.16)

которое равносильно дифференциальному уравнению

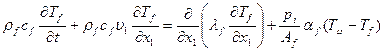(2.17)

В уравнение (2.17) входят две различные температуры, а именно, средняя по площади сечения жидкости температура T_f = T_f{x₁,t) и среднемассовая температура жидкости T_f = T_f{x₁,t). Верное равенство этих температур T_f = T _f достигается только в случае, когда профиль скорости 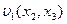однороден, т.е. практически не зависит от координат.

2.5.2. Уравнение баланса теплоты в стенке канала. Интегральное уравнение баланса теплоты в стенке канала для выделенного объема V_w имеет вид .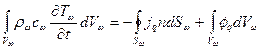

Здесь индекс 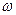означает, что все величины относятся к стенке канала.

Решение этих уравнений приводит к интегральному уравнению

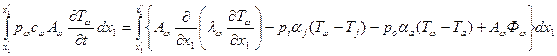, (2.18)

которое эквивалентно дифференциальному уравнению 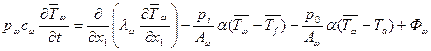. (2.19)

2.5.3 Граничные условия. В зависимости от задания на поверхности тела или жидкости температуры, теплового потока, конвективного теплооб­мена или контакта с другим телом или жидкостью, различают граничные условия первого, второго, третьего и четвертого родов. На поверхности мо­гут быть заданы и комбинации этих условий. Как и в работе [Модер] мы принимаем такиеже граничные условия.

Граничные условия первого рода. Если на поверхности S задано рас­пределение температуры Т(х, t), то говорят, что задано граничное условие 1 рода, т.е.

T = T(x,t), 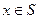. (2.20)

Граничное условие второго рода. При граничном условии 2 рода на поверхности задается вектор плотности теплового потока 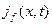, имеющий величину 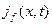. (2.21)

Граничное условие третьего рода. При граничном условии 3 рода на поверхности задается коэффициент теплоотдачи.

Граничное условие четвертого рода. При граничном условии 4 рода на поверхностях разных соприкасающихся фаз задаются температуры.

Контрольные вопросы, примеры и упражнения

1. Напишите граничное условие третьего рода через баланс теплоты.

2. Смысл и отличие средней по площади сечения жидкости температурыи среднемассовой температуры жидкости.

3. Что такое сопряженный конвективный теплообмен?

4. Сформулируйте уравнение непрерывности жидкости: при постоянной и переменной плотности вещества.

5. Почему уравнения баланса являются математической основой получения дифференциальных уравнений в частных производных?

6. Сформулируйте теорему Гаусса к поверхностному интегралу.

7. Перечислите основные причины диссипации энергии.

Дата добавления: 2014-12-27