Тепловое сопротивление теплопроводности

Тепловые сопротивления

Плотность потока теплоты в движущейся жидкости

Плотность потока переноса полевой величины

Рассмотрим жидкость с плотностью ρ, движущуюся со скоростью υ. Если в жидкости происходит перенос полевой величины А с плотностью полевой величины а = А/М (М- масса), то интенсивность переноса можно описать вектором плотности потока полевой величины А

q_А = ρаυ (1.12)

Векторное равенство (1.12) показывает, что вектор плотности полевой величины имеет длину равную

q_а = ρаυ (1.13)

и направлен вдоль вектора скорости потока υ.

Для потока массы А=М, а=М/М и плотность переноса массы равна

q_М = ρυ (1.14)

Для потока тепловой энергии Q с массовой плотностью q=Q/M плотность потока переноса энергии равна

q = ρqυ (1.15)

Поток переноса полевой величины еще называют конвективным потоком.

Перенос тепловой энергии в движущейся жидкости сопровождается двумя, одновременно протекающими процессами: теплопроводностью и конвекцией. При этом перенос теплоты теплопроводностью описывается законом Фурье, а перенос теплоты движущейся жидкостью - уравнением (1.2).

Вектор плотности теплового потока в движущейся жидкости равен

q = q + q = - λgrad T+ ρqυ. (1.16)

Понятия теплового сопротивления теплопроводности и конвекции, широко применяются в инженерных приложениях.

Тепловым сопротивлением называется величина равная отношению разности температур между двумя изотермическими поверхностями к тепловому потоку, протекающему между ними, т.е.

R_Т= (Т_а-Т_b)/Ф, К/Вт, (1.17)

где Т_а и Т_b- температуры изотермических поверхностей a и b; Ф - тепловой поток.

Плотность q(х) согласно закону Фурье (1.6) равна

q(x)= - λ(х) ,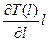

поэтому тепловой поток через поверхность S(l) может быть записан в виде

Ф = - λ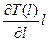(l) S(l)

или в виде

dТ(х) = -Ф .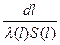

Интегрируя последнее равенство вдоль направления х от сечения a до сечения b и учитывая, что тепловой поток Ф на всем пути от a до b сохраняет свое значение, получим

Т_а-Т_b = Ф .

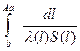Величина

R_T = (T_a-T_b)/Ф = 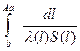, (1.18)

определяет тепловое сопротивление теплопроводности (кондукции) между двумя изотермическими поверхностями.

1.6.2. Конвективное тепловое сопротивление. Выделим на поверхности тела, взаимодействующего с окружающей средой участок площадью S. Примем, что температуры поверхности тела и среды во всех точках участка одинаковы и равны Т и Т_а соответственно. Тогда тепловой поток с поверхности тела в среду с учетом (1.3) равен

Ф = α(Т- Т_а)dS = (Т- Т_а) αdS.

Величина

R_T = (T_a-T_b)/Ф = ( αdS)^-1 (1.29)

равна конвективному тепловому сопротивлению и характеризует взаимодействие тела со средой.

Если коэффициент теплоотдачи не изменяется от точки к точке в пределах площади поверхности S, то тепловое сопротивление рассчитывается по формуле

R_T= (αS) ^-1 (1.30)

Тепловые сопротивления определяют расчетным путем или экспериментально.

Контрольные вопросы, примеры и упражнения

1. Чем отличаются стационарное и нестационарное температурное поле?

2. Что такое градиент температуры?

3. Сформулируйте основной закон теплопроводности – закон Фурье.

4. Как определить тепловое сопротивление теплопроводности?

5. Напишите формулу полного конвективного теплового сопротивления.

6. Рассмотрим теплопередачу через вертикальную пластину (толщиной δ, с коэффициентом теплопроводности λ), разделяющую две жидкости. Слева от пластины жидкость имеет температуру большую, чем справа от пластины. Теплообмен между жидкостью и поверхностью пластины подчиняется линейному закону Ньютона. Поток теплоты от горячей жидкости поступает на пластину, проходит через нее и далее поступает в холодную жидкость. Обозначим температуры и коэффициенты теплоотдачи горячей и холодной жидкости как Т_а1, α₁ и Т_α2, α₂ соответственно. Показать, что плотность теплового потока q от горячей жидкости к холодной может быть представлена в виде

q=k(Т_α1- Т_α2),

где k-коэффициент теплопередачи, равный

k=(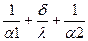)^-1.

Указание. Поскольку стационарное распределение температуры в пластине линейно, то нормальная производная в законе Фурье (1.12) равна

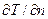=-(Т₁-Т₂)/δ.

где Т₁ и Т₂- температуры поверхностей пластины, Т₁>Т₂.

7.Показать, что тепловое сопротивление теплопроводности прямого цилиндра с коэффициентом теплопроводности λ, высотой h, площадью сечения А, теплоизолированного с боковой поверхности определяется по формуле

R_T= h/ λА.

8. Показать, что тепловое сопротивление теплопроводности кругового (полого цилиндра высотой h и коэффициентом теплопроводности λ) от внутренней поверхности к наружной, заданным равномерным распределением температуры на внутренней (Т₁) и внешней (Т₂) поверхностях (Т₁>Т₂) дается выражением

R_{T= ,}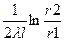

где r₁ и r₂- радиусы внутренней и внешней поверхностей цилиндра. Торцы цилиндра - теплоизолированы.

Указание. Учесть, что температурное поле цилиндра не изменяется по высоте, в цилиндрических координатах одномерно и является только функцией радиуса цилиндра (изотермические поверхности – концентрические окружности).

8. Рассмотрим теплопередачу через круговой полный цилиндр высотой h, с коэффициентом теплопроводности λ; торцы цилиндра теплоизолированы. Внутренняя поверхность цилиндра радиуса r₁ и внешняя поверхность цилиндра радиуса r₂ омывается жидкостями с температурами Т_α1, Т_α2 (Т_α1>Т_α2) соответственно. Взаимодействие жидкостей и поверхностей цилиндра подчиняется закону Ньютона с коэффициентами теплоотдачи α₁ и α₂. Тепловой поток от жидкости внутри цилиндра поступает на его внутреннюю поверхность, рассеивается внутри цилиндра и далее поступает в жидкость снаружи цилиндра.

Показать, что тепловой поток от горячей жидкости к холодной может быть представлен в виде

Ф = kπh (Т_α1- Т_α2),

где k- коэффициент теплопередачи, равный

k = ()^-1.

Указание. Учесть, что потерь теплового потока, при прохождении его от горячей жидкости к холодной, не происходит.

Дата добавления: 2014-12-27