Тепловой поток и плотность теплового потока

Найдем поток теплоты через элемент поверхности dS и поверхность S. Согласно определению, вектор плотности теплового потока q направлен перпендикулярно к элементарной площадке dS_┴, через которую он протекает и равен отношению теплового потока к величине dS_┴. Величина теплового потока dФ через элементарную площадку dS_┴ равна

dФ = qdS_┴. (1.1)

Поток теплоты dФ через всю поверхность S получается суммирование вкладов от всех элементов поверхности и равен

Ф = qdS= qdS – (1.2)

для незамкнутой поверхности S, и

Ф = qndS= qdS – (1.3.)

для замкнутой поверхности S.

Рис.1.1. Тело, ограниченное поверхностью S и разделенное на три части.

Далее будем считать тепловой поток положительным, если он вытекает из объема, и отрицательным – если втекает внутрь объема.

Покажем справедливость важного свойства потока теплоты, которое используется в дальнейшем при разработке численного метода теплового баланса: поток теплоты через поверхность тела равен сумме потоков теплоты через поверхности всех его частей.

Возьмем тело, ограниченное поверхностью S (рис. 1.1).

Разделим его, например, на три части двумя сечениями ab и bc. Первое тело (а) ограничено частью внешней поверхности S_а и сечением σ_ab; второе тело (b) ограничено частью внешней поверхности S_b и сечениями σ_ab и σ_bc; третье тело (с) ограничено частью внешней поверхности S_c и сечением σ_bc. Потоки теплоты через поверхности равны:

- для тела а

qdS_а + 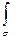qdσ_ab,

- для тела b

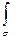qdσ_ab+ qdS_b+ 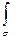qdσ_bc,

- для тела с

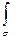qdσ_bc+ qdS_c.

Складывая эти три равенства получим сумму

qdS_а+ qdS_b+ qdS_c,

которая, принимая во внимание, что S=S_а +S_b+S_c, равна

Дата добавления: 2014-12-27