Общее уравнение баланса

Методологические основы составления уравнений теплового баланса

Уравнения баланса являются математической основой получения дифференциальных уравнений в частных производных, описывающих процессы переноса различных полевых величин. В то же время интегральные уравнения баланса позволяют просто и естественно построить эффективный численный метод расчета температурных полей в объектах сложной формы.

Рассмотрим твердое тело или жидкость, в которых распределена полевая величина А, с удельной величиной а, равной величине А, отнесенной к единице массы. Полевая величина А в объеме V равна

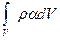
Ее изменение во времени

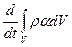
может быть вызвано либо втеканием или вытеканием потока Q_а величины А в объем V или из него через поверхность S

Q_а= q_аndS,

либо возникновением или уменьшением полевой величины А за счет существования в объеме V источников или стоков полевой величины А

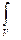ф_adV,

где ф_a – объемная плотность внутреннего источника полевой величины А, равная изменению полевой величины в единице объема за единицу времени; q_а – вектор плотности потока величины а. Будем считать, что направление потока q_а положительно, т.е. вытекает из объема.

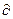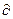Поскольку выделенный объем V неподвижен, то полная производная по времени d(ρa)/dt равна локальной производной по времени (ρa)/ t.

Тогда получим общее уравнение баланса полевой величины А в интегральной форме

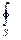= - q_аndS+ 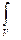ф_adV. (2.1)

Из общего уравнения баланса в интегральной форме непосредственно следует дифференциальная форма уравнения баланса для любой точки тела. Действительно, применяя теорему Гаусса к поверхностному интегралу в правой части (2.1) получим

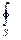q_аndS= q_аdV. (2.2)

Перенося правые члены в (2.1) влево, с учетом (2.2) получим соотношение

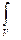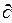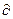{ (ρa)/ t+div q_а-ф_a}dV=0,

которое должно быть справедливо для любого выделенного объема. Отсюда получаем дифференциальное уравнение

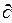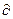(ρa)/ t+div q_а= ф_a, (2.3)

являющиеся уравнением баланса полевой величины А в любой точке тела.

Дата добавления: 2014-12-27