Выявление стратегии, сводящей к минимуму риски игроков

ПРИЕМЫ РЕШЕНИЯ МАТРИЧНЫХ ЗАДАЧ ТЕОРИИ ИГР С НУЛЕВОЙ СУММОЙ

Получатель (т. е. первый игрок, выбирающий строку в платежной матрице), не склонный к риску, выделяет в каждой строке платежной матрицы наименьшее значение. Из всех этих наименьших значений выбирается наибольшее (оно называется нижней ценой игры и обозначается α, максимином).

Плательщик (т. е. второй игрок, выбирающий столбец), не склонный к риску, выделяет в каждом столбце платежной матрицы наибольшее значение. Из всех наибольших значений выбирается наименьшее (оно называется верхней ценой игры и обозначается β, минимаксом).

Так как даже наибольшее из наименьших значений не может превзойти наименьшего из наибольших значений (независимо от того, по строкам или по столбцам происходил отбор), то для верхней и нижней цен игры справедливо соотношение: a £ b.

Пример 1а. Количество возможных стратегий Получателя – 5, Плательщика – 4. Величины платежа образуют таблицу.

	В 1	В 2	В 3	В 4
А 1
А 2	-2	-4	-2
А 3				-3
А 4	-1
А 5

Требуется найти наиболее выгодную стратегию Получателя.

Решение

1. В каждой строке найдем минимальное значение

	В 1	В 2	В 3	В 4		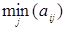Расшифровка
А 1						a1 = min(2; 3; 5; 9) = 2;
А 2	-2	-4	-2		-4	a2 = min(-2; -4; -2; 7) = -4;
А 3				-3	-3	a3 = min(7; 5; 0; -3) = -3;
А 4	-1				-1	a4 = min(-1; 6; 1; 2) = -1;
А 5						a5 = min(6; 9; 6; 3) = 3.

2. Вычислим максимин

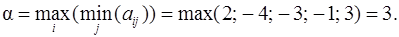
Найденное значение реализуется при выборе последней (пятой) стратегии А 5 Получателя (она выделена в таблице).

Ответ: наиболее выгодной для Получателя (при однократной игре) является стратегия А 5, так как при любом выборе Плательщиком его стратегии величина платежа составит a = 3 или больше.

Пример 1б. В задаче с предыдущими условиями (см. пример 1а) требуется найти наиболее выгодную стратегию Плательщика.

Решение

1. В каждом столбце найдем максимальное значение.

	В 1	В 2	В 3	В 4		Расшифровка
А 1						b1 = max(2; -2; 7; -1; 6) = 7;
А 2	-2	-4	-2			b2 = max(3; -4; 5; 6; 9) = 9;
А 3				-3		b3 = max(5; -2; 0; 1; 6) = 6;
А 4	-1					b4 = max(9; 7; -3; 2; 3) = 9.
А 5

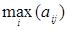
2. Вычислим минимакс

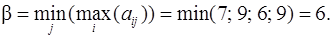
Найденное значение реализуется при выборе третьей стратегии В 3 Плательщика (она выделена в таблице).

Ответ: наиболее выгодной для Плательщика (при однократной игре) является стратегия В 3, так как при любом выборе Получателем его стратегии величина платежа составит b = 6 или меньше.

2.2. Чистые и смешанные стратегии игроков. Установление ситуаций, когда задача имеет решение «в чистых стратегиях»

Из рассмотрения предыдущих задач видно, что Получатель может добиться гарантированного результата игры не меньше, чем α, а Плательщик – не больше, чем β. С другой стороны, из определения этих величин следует, что a £ b. Таким образом, при точном равенстве между верхней и нижней ценами игры ожидается постоянный выбор игроками наиболее выгодных для них стратегий (т. е. игра решается в чистых стратегиях или имеет седловую точку) независимо от количества актов, и цена игры n определяется равенством a = n = b. Активными стратегиями игроков являются только те, в которых реализуется цена игры.

В остальных случаях, когда верхняя и нижняя цены игры различаются (как в примерах 1а и 1б), часто появляется возможность достижения промежуточного, более выгодного результата n > a для Получателя и (или) n < b для Плательщика в серии многократных игр. Для этого применяются смешанные стратегии: несколько чистых стратегий используются с разной вероятностью, причем то, какая именно стратегия будет применяться в следующий раз, игроки держат втайне.

Теория матричных игр (см. последующие приемы) помогает определить состав чистых стратегий, образующих смешанную стратегию (активные стратегии), предсказать вероятности их использования и средний результат по серии игр (т. е. цену игры n), но не отдельный результат в серии. Фактический результат приближается к теоретическому предсказанию при увеличении количества актов игры и отсутствии утечек информации о выборе стратегий игроками.

Пример 2. ( игра, имеющая решение в чистых стратегиях). Требуется найти наиболее выгодные стратегии игроков, если дана платежная матрица.

	В 1	В 2	В 3
А 1
А 2	-2	-2
А 3			-3

Решение

1. Определим наименьшие значения в строках и наибольшие значения в столбцах матрицы.

	В 1	В 2	В 3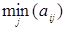
А 1
А 2	-2	-2		-2
А 3			-3	-3

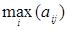
2. Вычислим максимин и минимакс

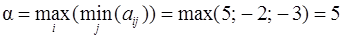
(реализуется при выборе Получателем стратегии А 1),

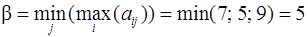
(реализуется при выборе Плательщиком стратегии В 2).

3. Так как a = b, определим цену игры

n = a = b = 5.

Ответ:наиболее выгодная стратегия Получателя – А 1; наиболее выгодная стратегия Плательщика – B 2.

Интерпретация результата: получатель, выбирая стратегию А 1 (т. е. строку № 1) гарантирует результат игры n ³ 5. С другой стороны, Плательщик, выбирая стратегию В 2 (т. е. столбец № 2) гарантирует результат игры n £ 5. Таким образом, цена игры n = 5 совпадает с верхней и нижней ценами игры. Никакая смешанная стратегия не принесет пользы ни Получателю, ни Плательщику: любое использование Получателем стратегий А 2 и А 3 (при сохранении Плательщиком стратегии В 2) невыгодно Получателю, но и любое использование Плательщиком стратегий В 1 и В 3 (при сохранении Получателем стратегии А 1) невыгодно Плательщику.

2.3. Исключение стратегий, заведомо невыгодных для игроков
(по сравнению с другими возможными чистыми стратегиями)

Применение универсальных приемов (см. далее) поиска смешанных стратегий и цены игры предполагает проведение рутинных и громоздких вычислительных процедур, существенно зависящих от количества стратегий, имеющихся у игроков. Поэтому, если только есть такая возможность, следует освободить задачу от тех стратегий, которые заведомо не будут использоваться игроками, так как другие стратегии являются для них более выгодными. Такие стратегии вычеркиваются из платежной матрицы (желательно при этом сохранять обозначения стратегий, так как предполагается проверка найденного решения на всей исходной матрице, а не только на множестве «активных» стратегий).

Дата добавления: 2014-12-27