Графическое сравнение зависимостей результата игры от вероятности применения вторым игроком чистых стратегий – выявление активных стратегий первого игрока

Замечания

При упрощении матрицы сохранились верхняя и нижняя цены игры

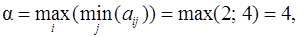
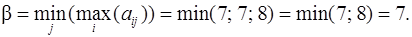
Точный результат решения задачи (читатель может восстановить процесс расчета самостоятельно на основе п. 2.5 или сравнить результат с примерами 6а и 6б, где вероятности применения Плательщиком его стратегий В 2 и В 3 обозначаются y ₂ и y ₃)

Значение вероятности x _2опт (а затем x _1опт = 1 – x _2опт ) и цены игры n = m_опт, может быть получено из системы уравнений

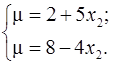
Введем обозначения: y ₁ – вероятность применения Плательщиком стратегии В 1, т. е. доля случаев, когда Плательщик намеревается использовать стратегию В 1 в общем количестве проводимых игр. Аналогично, y ₂ – вероятность применения Получателем стратегии В 2; она непосредственно связана с y ₁ соотношением y ₁ + y ₂ = 1. Например, если в каждой сотне игр Получатель собирается использовать стратегию В 1 27 раз, то y ₁ = 0,27; стратегия В 2 будет использована 73 раза и y ₂ = 0,73.

Допустим, что Получатель наряду с другими своими стратегиями достаточно много раз применяет стратегию А 1. Тогда платежи определяются первой строкой платежной матрицы, средняя величина m _{A 1} таких платежей может быть вычислена

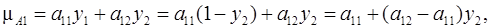
где a ₁₁ и a ₁₂ – элементы первой строки платежной матрицы.

Данная зависимость – линейная, на координатной плоскости (по оси абсцисс отложена y ₂, а по оси ординат – средняя величина платежа) ей соответствует отрезок прямой, соединяющий точки (0; a ₁₁) и (1; a ₁₂).

Таким образом, каждая стратегия Получателя отображается одним отрезком на плоскости. Если одна из стратегий является заведомо невыгодной для Получателя по сравнению с другой, то весь соответствующий отрезок расположен выше другого отрезка. Отрезки, отвечающие предпочитаемым Получателем стратегиям, пересекаются между собой и образуют ломаную кривую, над которой нет других отрезков.

Как и в случае с однократным взаимодействием, Плательщик заинтересован в минимизации среднего (по серии игр) наибольшего из возможных платежей и может использовать для этого выбор вероятности применения своих двух стратегий. Точка (y _2опт; n) соответствует одной из точек пересечения отрезков, характеризующих чистыестратегии Получателя. Гарантией того, что своим выбором стратегии Получатель не может увеличить величину среднего платежа, является наглядный факт: выше данной точки не расположен ни один отрезок.

С учетом найденной смешанной стратегии Плательщика, можно выделить стратегии, которые будут использованы Получателем в его смешанной стратегии – именно соответствующие им отрезки проходят через точку (y _2опт; n).

Пример 4б. Требуется приближенно определить смешанную стратегию Плательщика и цену игры, выявить состав смешанной стратегии Получателя и провести упрощение данной платежной матрицы (она получена транспонированием матрицы из примера 4а)

	В 1	В 2
А 1
А 2
А 3

Решение

1. Найдем точки для построения графика

	y 2 = 0	y 2 = 1
А 1 (m = 7 – 2 y 2)	(0; 7),	(1; 5)
А 2 (m = 2 + 5 y 2)	(0; 2),	(1; 7)
А 3 (m = 8 – 4 y 2)	(0; 8),	(1; 4)

2. Выполним графическое построение

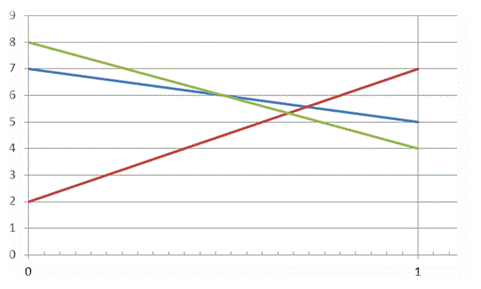
3. По результатам построения сделаем выводы.

Верхний край фигуры, над которым нет уже никаких отрезков, образован отрезками, соответствующими стратегиям Получателя А 3, А 1 и А 2 (слева направо). Эти отрезки пересекаются в точках L и M.

Низшая точка описанной выше ломаной – точка М с примерными координатами (0,7; 5,6). Она является точкой пересечения отрезков, соответствующих стратегиям Получателя А 1 и А 2, значит, эти стратегии являются активными.

Применение стратегии В 1 с вероятностью y _1опт» 1 – 0,7 = 0,3 и стратегии В 2 с вероятностью y _2опт» 0,7 гарантирует Плательщику средний платеж в размере n» 5,6 (или меньше).

Стратегия А 3 использоваться Получателем не будет, так как (при найденной смешанной стратегии Плательщика) средняя величина платежа в таких актах взаимодействия окажется невыгодной, так как меньше значения n» 5,6. Смешанная стратегия Получателя состоит в сочетании его чистых стратегий А 1 и А 2. Таким образом, из платежной матрицы можно вычеркнуть строку, соответствующую стратегии A 3 (она выделена в таблице).

	В 1	В 2			В 1	В 2
А 1				А 1
А 2			~	А 2
А 3

Ответ:

– вероятности применения стратегий Плательщика B 1 – y_1опт » 0,3 и B 2 – y_2опт » 0,7;

– цена игры n» 5,6;

– смешанная стратегия Получателя состоит в применении его чистых стратегий А 1 и А 2, стратегии являются активными (строку, соответствующую неактивной стратегии Получателя А 3, можно исключить из платежной матрицы).

Дата добавления: 2014-12-27