
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторный анализ. Кратные, криволинейные и поверхностные интегралы
|
|
|
|
Кратные, криволинейные и поверхностные интегралы.
261-270. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах 
261.  . 262.
. 262. 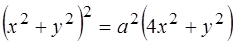 .
.
263. 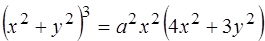 . 264.
. 264.  .
.
265.  . 266.
. 266. 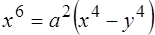 .
.
267.  . 268.
. 268. 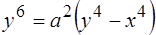 .
.
269.  . 270.
. 270.  .
.
271-280. Вычислить с помощью тройного интеграла объём тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость ХОY.
271. 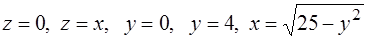 .
.
272. 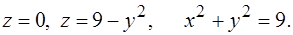
273. 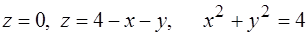 .
.
274.  .
.
275. 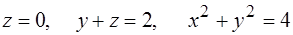 .
.
276.  .
.
277.  .
.
278. 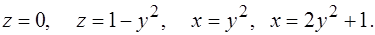
279. 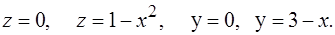
280. 
281.Вычислить криволинейный интеграл 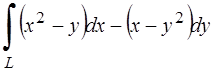 вдоль дуги
вдоль дуги  окружности
окружности  ,
,  , обходя её против хода часовой стрелки от точки
, обходя её против хода часовой стрелки от точки  до точки
до точки  . Сделать чертеж.
. Сделать чертеж.
282.Вычислить криволинейный интеграл  вдоль ломанной
вдоль ломанной  где
где  . Сделать чертёж.
. Сделать чертёж.
283.Вычислить криволинейный интеграл  вдоль границы
вдоль границы  треугольника
треугольника  , обходя её против хода часовой стрелки, если
, обходя её против хода часовой стрелки, если 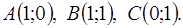 Сделать чертёж.
Сделать чертёж.
284.Вычислить криволинейный интеграл 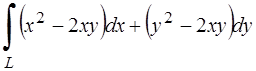 вдоль дуги
вдоль дуги  параболы
параболы  от точки
от точки 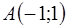 до точки
до точки  . Сделать чертеж.
. Сделать чертеж.
285.Вычислить криволинейный интеграл 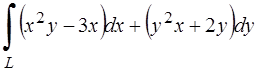 вдоль верхней половины
вдоль верхней половины  эллипса
эллипса 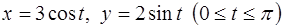 . Сделать чертеж.
. Сделать чертеж.
286.Вычислить криволинейный интеграл 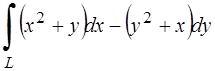 вдоль ломаной
вдоль ломаной  где
где  . Сделать чертеж.
. Сделать чертеж.
287.Вычислить криволинейный интеграл  вдоль дуги
вдоль дуги  кривой
кривой 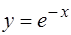 от точки
от точки 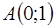 до точки
до точки  . Сделать чертёж.
. Сделать чертёж.
288.Вычислить криволинейный интеграл 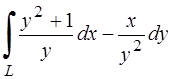 вдоль отрезка
вдоль отрезка  прямой от точки
прямой от точки 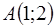 до точки
до точки  . Сделать чертёж.
. Сделать чертёж.
289.Вычислить криволинейный интеграл 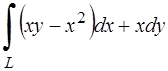 вдоль дуги
вдоль дуги  параболы
параболы 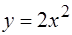 от точки
от точки  до точки
до точки 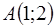 . Сделать чертёж.
. Сделать чертёж.
290.Вычислить криволинейный интеграл  вдоль дуги
вдоль дуги  кривой
кривой  от точки
от точки  до точки
до точки  . Сделать чертёж.
. Сделать чертёж.
291-300.Даны векторное поле  и плоскость Ax + By + Cz + D = 0(p), которая совместно с координатными плоскостями образует пирамиду V. Пусть
и плоскость Ax + By + Cz + D = 0(p), которая совместно с координатными плоскостями образует пирамиду V. Пусть  - основание пирамиды, принадлежащее плоскости (p);
- основание пирамиды, принадлежащее плоскости (p); 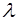 -контур, ограничивающий
-контур, ограничивающий  ;
; 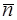 -нормаль к
-нормаль к  , направленная вне пирамиды V. Требуется вычислить:
, направленная вне пирамиды V. Требуется вычислить:
1) поток векторного поля  через поверхность
через поверхность  в направлении нормали
в направлении нормали 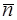 ;
;
2) циркуляцию векторного поля  по замкнутому контуру
по замкнутому контуру 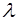 непосредственно и применив теорему Стокса к контуру
непосредственно и применив теорему Стокса к контуру 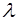 и ограниченной им поверхности
и ограниченной им поверхности  с нормалью
с нормалью 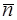 .
.
3) поток векторного поля  через полную поверхность пирамиды V в направлении внешней нормали к ее поверхности непосредственно, применив теорему Остроградского. Сделать чертеж.
через полную поверхность пирамиды V в направлении внешней нормали к ее поверхности непосредственно, применив теорему Остроградского. Сделать чертеж.
291. 
292. 
293. 
294. 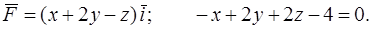
295. 
296. 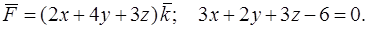
297. 
298. 
299. 
300. 
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 587; Нарушение авторских прав?; Мы поможем в написании вашей работы!