Теория вероятностей и математическая статистика

Ряды

Дифференциальные уравнения

301-310. Найти общее решение дифференциального уравнения 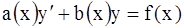и частное решение, удовлетворяющее начальному условию при .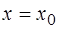

301. .

302. .

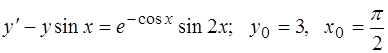303. .

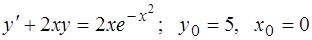304. .

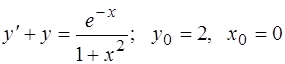305. .

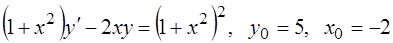306. .

307. .

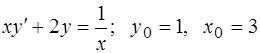308. .

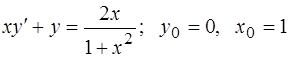309. .

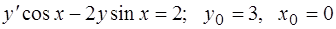310. .

311-330. Найти общее решение дифференциального уравнения

311. 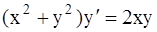. 312. .

313. 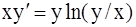. 314. .

315. 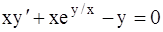. 316. .

317. . 318. .

319. . 320. .

321. 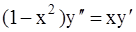. 322. .

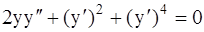323. 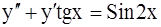. 324. .

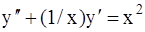325. . 326. .

327. . 328. .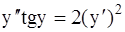

329. . 330. .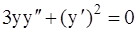

331-340. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям 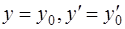при .

331. .

332. .

333. .

334. .

335. .

336. .

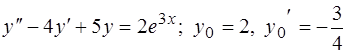337. .

338. .

339. .

340. .

341-350.Найти частное решение дифференциального уравнения,

удовлетворяющее начальным условиям .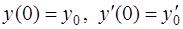

341.

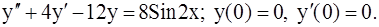
342.

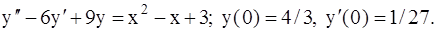
343.

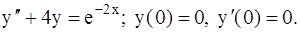
344.

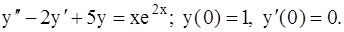
345.

346.

347.

348.

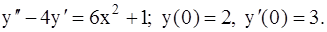
349.

350.

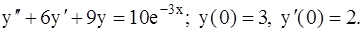
351-360.Исследовать сходимость числового ряда .

351. 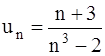. 352. .

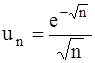353. . 354. .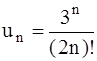

355. . 356. .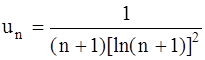

357. 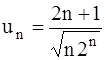. 358. .

359. 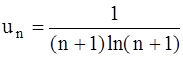. 360. .

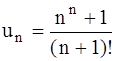361-370. Найти интервал сходимости степенного ряда .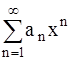

361. 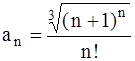362.

363. 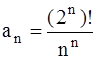364.

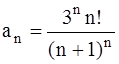
365. 366.

367. 368.

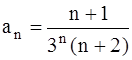
369. 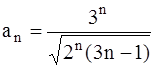370.

371-380.Написать три первых члена степенного ряда по заданному общему члену 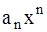, где 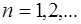; найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.

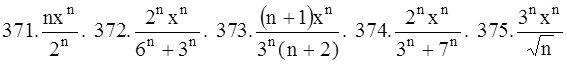
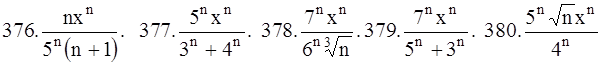
381-390.Вычислить определенный интеграл 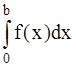с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

381. 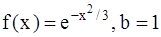. 382. .

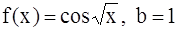383. . 384. .

385. . 386. .

387. . 388. .

389. 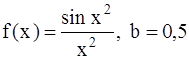. 390.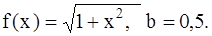

391-395. Выразить определенный интеграл 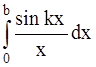в виде сходящего ряда, используя ряд Маклорена для подынтегральной функции. Найти приближенное значение этого интеграла с точностью до .

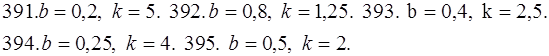
396-400. Выразить определенный интеграл в виде сходящегося ряда, используя ряд Маклорена для подынтегральной функции. Найти приближенное значение этого интеграла с точностью до 0,001.

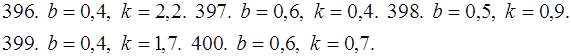
I. 401-450

401.Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что студент знает:

а) все три вопроса; б) только два вопроса; в) только один вопрос экзаменационного вопроса.

402.В каждой из двух урн находится 5 белых и 10 черных шаров. Из первой урны переложили во вторую наудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным.

403.Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,9, вторым - 0,8, третьим - 0,7. Найти вероятность того, что:

а) только один из стрелков попал в цель; б) только два стрелка попали в цель; в) все три стрелка попали в цель.

404.Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 1600 испытаниях событие наступит 1200 раз.

405.Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе - 0,95, третье - 0,85. Найти вероятность того, что при аварии сработает: а) только одно устройство; б) только два устройства; в) все три устройства.

406.Вероятность наступления события в каждом из одинаковых и независимых испытаниях равна 0,02. Найти вероятность того, что в 150 испытаниях событие наступит 5 раз.

407.В партии из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50 изделий, взятых наудачу из этой партии, ровно три окажутся дефектными.

408.Вероятность наступления события в каждом из одинаковых и независимых испытаниях равна 0,8. Найти вероятность того, что в 125 испытаниях событие наступит не менее 75 раз и не более 90 раз.

409.На трех станках при одинаковых и независимых условиях изготавливаются детали одного наименования. На первом станке изготавливается 10 %, на втором – 30 %, на третьем – 60 % всех деталей. Вероятность каждой детали быть бездефектной равна 0,7, если она изготовлена на первом станке, 0,8 - если на втором станке и 0,9 - если на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.

410.Два брата входят в состав двух спортивных команд, состоящих из 12 человек каждая. В двух урнах имеются по 12 билетов с номерами от 1 до 12. Члены каждой команды вынимают наудачу по одному билету из определенной урны (без возвращения). Найти вероятность того, что оба брата вытащат билет номер 6.

411-420. Дискретная случайная величина X может принимать только два значения и , причем 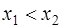Известны вероятность возможного значения , математическое ожидание M(X) и дисперсия Д(X). Найти закон распределения этой случайной величины.

411. =0,1; M(X)=3,9; Д(X)=0,09.

412. =0,3; M(X)=3,7; Д(X)=0,21.

413. =0,5; M(X)=3,5; Д(X)=0,25.

414. =0,7; M(X)=3,3; Д(X)=0,21.

415. =0,9; M(X)=3,1; Д(X)=0,09.

416. =0,9; M(X)=2,2; Д(X)=0,36.

417. =0,8; M(X)=3,2; Д(X)=0,16.

418. =0,6; M(X)=3,4; Д(X)=0,24.

419. =0,4; M(X)=3,6; Д(X)=0,24.

420. =0,2; M(X)=3,8; Д(X)=0,16.

421-430.Случайная величина X задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.

421. 422.

423. 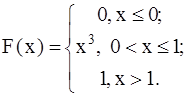424.

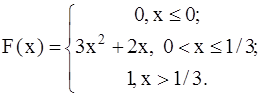
425. 426.

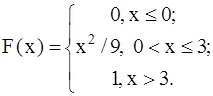
427. 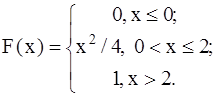428.

429. 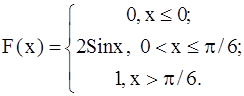430.

431-440.Известны математическое ожидание a и среднее квадратическое отклонение нормально распределенной случайной величины X. Найти вероятность попадания этой величины в заданный интервал .

431. 432.

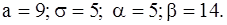
433. 434.

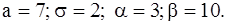
435. 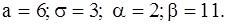436.

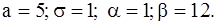
437. 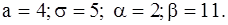438.

439. 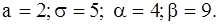440.

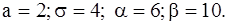
441-450.Найти доверительный интервал для оценки математического ожидания 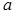нормального распределения с надежностью 0,95, зная выборочную среднюю , объемом выборки n и среднее квадратическое отклонение .

441. 442.

443. 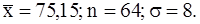444.

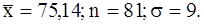
445. 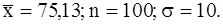446.

447. 448.

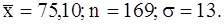
449. 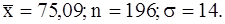450.

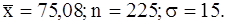
Дата добавления: 2014-12-27