Стереометрия

Признак параллельности прямых. Если две прямые параллельны третьей прямой, то они параллельны.

Признак параллельности прямой и плоскости. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Теорема о трех перпендикулярах. Прямая, проведенная в плоскости через основание наклонной перпендикулярна к ее проекциям на плоскость, перпендикулярна и к самой наклонной.

Обратная теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

Признак перпендикулярности плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Теорема 1. Если двугранные углы при основании пирамиды равны, то центр вписанного шара принадлежит ее высоте.

Теорема 2. Если боковые ребра пирамиды равны, то центр описанного шара лежит на высоте или ее продолжении.

Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Определение. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.

Определение. Двугранным углом называется фигура в пространстве, образованная двумя полуплоскостями, исходящими из одной прямой. Полуплоскости называются гранями двугранного угла, а их общая прямая – ребром двугранного угла.

Двугранный угол измеряется линейным углом, т.е. углом между двумя перпендикулярами к ребру, выходящими из одной точки и лежащими в разных гранях.

Определение. Общим перпендикуляром двух скрещивающихся прямых называется отрезок, концы которого лежат на данных прямых, перпендикулярные к ним.

Определение. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.

Определение. Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.

Определение. Апофемой правильной пирамиды называется высота ее боковой грани, проведенная из вершины пирамиды.

Теорема 3. Если двугранные углы при основании пирамиды равны 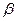, то высота пирамиды проектируется в центр окружности, вписанной в основание пирамиды. И при этом

Рисунок 21

Теорема 4. Если боковые ребра пирамиды равны, то центр описанного шара лежит на высоте или ее продолжении.

Теорема 5. Если боковые ребра пирамиды равны, то центр описанного шара лежит на высоте или ее продолжении.

Теорема 6. Если боковые ребра пирамиды равны или одинаково наклонены к плоскости основания, то высота пирамиды проектируется в центр окружности, описанной около основания.

Определение. Прямая призма называется правильной, если ее основания – правильные многоугольники.

Определение. Перпендикулярным сечением наклонной призмы называется ее сечение плоскостью, пересекающей все боковые ребра призмы и перпендикулярной к ним.

Дата добавления: 2014-12-27