
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тригонометрия
|
|
|
|
Правила нахождения области определения и множества значений функции
Область определения функции
 , то , то  . .
 ,то ,то  . .
 , то , то 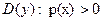 . .
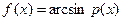 , то , то  . .
 , то , то  . .
 , то , то  . .
 , то , то 
| (20) | |
Множество значений функции
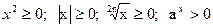 ; ;  . .

 . .


| (21) |
Пример. Найти область определения функции 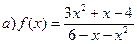 ,
, 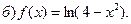
►а) 
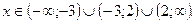
б) 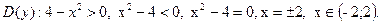
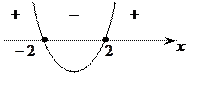
Рисунок 11
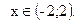 ◄
◄
4.1. Углы измеряются в градусах и радианах, соотношение между ними
1800= 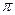 радиан
радиан
Поэтому 10= 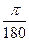 радиан и 1 радиан=
радиан и 1 радиан=  градусов.
градусов.
4.2. Угол, отложенный по часовой стрелке, считается отрицательным, а угол, отложенный против часовой стрелки, считается положительным.
Будем откладывать углы от положительного направления оси Ox.
4.3. Круг, с центром в начале координат и радиусом 1, называется единичным или тригонометрическим кругом.
4.4. Каждому углу 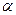 соответствует точка
соответствует точка  , ее координаты называются соответственно косинусом и синусом угла
, ее координаты называются соответственно косинусом и синусом угла 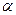 :
:

Рисунок 12
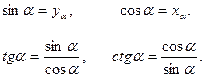
4.5. В прямоугольном треугольнике:
Синус угла есть отношение противолежащего катета к гипотенузе.
Косинус угла есть отношение прилежащего катета угла к гипотенузе.
Тангенс угла есть отношение противолежащего катета к прилежащему катету.
Котангенс угла есть отношение прилежащего катета к противолежащему катету.
4.6. Область определения тригонометрических функций
D ( )=
)=  D (
D (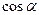 )=
)= 
D (tg 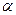 ):
):  D (ctg
D (ctg 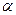 ):
): 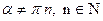
D (tg 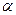 .ctg
.ctg 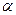 ):
): 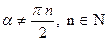
4.7. Множество значений тригонометрических функций
 , т.е.
, т.е. 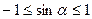
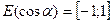 , т.е.
, т.е. 
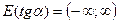

4.8. Периодичность тригонометрических функций
 и
и 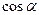 есть периодические функции с наименьшим периодом
есть периодические функции с наименьшим периодом  и
и
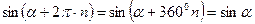
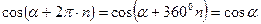
 и
и 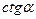 есть периодические функции с наименьшим периодом
есть периодические функции с наименьшим периодом 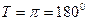 и
и

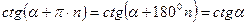
4.9. Знаки тригонометрических функций

Рисунок 13
4.10. Четность тригонометрических функций
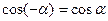 — функция четная
— функция четная
 — функция нечетная
— функция нечетная
 — функция нечетная
— функция нечетная
 — функция нечетная
— функция нечетная
4.11. Формулы приведения. Они позволяют отбросить числа  , пользуясь двумя правилами:
, пользуясь двумя правилами:
1) находим четверть, в которой расположен угол, и определяем знак приводимой функции в этой четверти и ставим его перед приведенной функцией;
2) меняем функцию на кофункцию, если аргументом являются углы  или
или  , т.е. если отбрасываем угол
, т.е. если отбрасываем угол 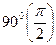 или
или 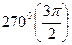 ;
;
3) не меняем название функции, если аргументом являются углы 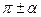 или
или 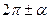 , т.е. если отбрасываем угол
, т.е. если отбрасываем угол 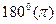 или
или 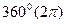 .
.
4.12. Тригонометрические функции одного и того же угла.
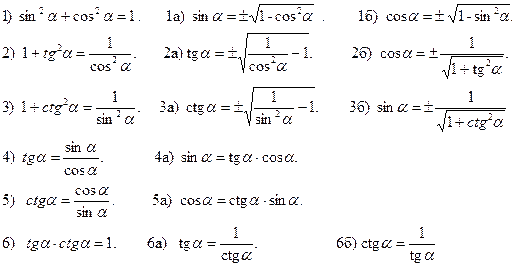
4.13. Формулы сложения
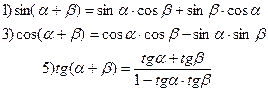
| 
|
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1713; Нарушение авторских прав?; Мы поможем в написании вашей работы!