Студопедия

КАТЕГОРИИ:

Главная
Случайная страница
Познавательное
Новые статьи
Контакты
Заказать работу

Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)

Перевод чисел из десятичной системы счисления в любую другую


⇐ Предыдущая234567891011Следующая ⇒


Для перевода чисел из десятичной с/с в любую другую, необходимо делить десятичное число на основание системы, в которую переводят, сохраняя при этом остатки от каждого деления.

Результат формируется справа налево. Деление продолжается до тех пор, пока результат деления не станет меньше делителя.

Пример 9. Перевести число 13 из десятичной системы счисления в двоичную систему:

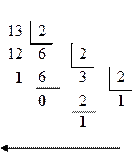
13(10) => 1101(2).

Пример 10. Перевести число 13 из десятичной системы счисления в восьмеричную систему:

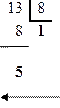
13(10) => 15(8).

Пример 11. Перевести число 638 из десятичной системы счисления в шестнадцатеричную систему:

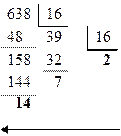
638(10) => 27E(16).

Остатки записываются в шестнадцатеричном виде (14 => Е).

Пример 12. Сложение двоичных чисел:

11011001(2)

+ 1011101(2)

100110110(2).

Для проверки результата сложения двоичное число нужно разбить на триады, перевести в восьмеричную систему счисления согласно таблице 1, а затем перейти в десятичную систему и осуществить сложение.

11 011 001(2)=331(8)=3*82+3*81+1*80=192+24+1=217(10).

1 011 101(2)=135(8)=1*82+3*81+5*80=64+24+5=93(10).

100 110 110(2)=466(8)=4*82+6*81+6*80=256+48+6=310(10).

Проверка:

217(10)+93(10)=310(10).

 

Пример 13. Сложение шестнадцатеричных чисел:

8E38C(16)

+ 5D35(16)

940C1(16).

Перед сложением необходимо перейти согласно таблице 1 в 10-ю систему счисления, произвести сложение, затем опять вернуться к 16-ой системе счисления.

C(16)+5(16) => 12(10)+5(10)=17(10) => 11(16).

8(16)+3(16)+1(16)=12(10) => С(16).

3(16)+D(16)=3(10)+13(10)=16(10) => 10(16).

E(16)+5(16)+1(16)=14(10)+5(10)+1(10)=20(10) =>14(16).

8(16)+1=9(10) => 9(16).

Вопросы для самоконтроля

  1. Что такое система счисления?
  2. Чем характеризуется система счисления?
  3. Виды систем счисления.
  4. Десятичная система счисления. Основание. Представление чисел.
  5. Двоичная система счисления. Основание.
  6. Восьмеричная и шестнадцатеричная системы счисления.
  7. Перевод чисел из любой системы счисления в десятичную.
  8. Перевод чисел из десятичной в любую другую систему счисления.
  9. Почему для машинной арифметики используется двоичная система счисления?

Методические указания для выполнения практического задания №1. «Системы счисления»

Цель работы: Ознакомиться с системами счислений. Рассмотреть систему представления чисел в памяти ЭВМ.

Задание:

  1. В приложении 1 выбрать вариант задания.
  2. Выполнить задание, пользуясь теоретическими сведениями.
  3. Оформить выполненное задание в тетради для практических занятий.
  4. Результат работы предъявить преподавателю.
  5. Ответить на вопросы самоконтроля.
  6. Защитить выполненную работу у преподавателя.

 


Приложение 1. Таблица вариантов заданий

Вариант Задание
 
  1. Выполнить действия в двоичной системе счисления:
· 1100 – 0111 · 11001*111 · 1111 + 1011
  1. Перевести из одной системы счисления в другую:
  • число 42 из десятичной системы счисления в 2-ную
  • число 100111 из двоичной системы счисления в 10-ную
  • число FA2 из шестнадцатеричной системы счисления в 5-ную
 
  1. Выполнить действия в двоичной системе счисления:
  • 1111 – 1101
  • 1001 * 110
  • 10111 + 111
  1. Перевести из одной системы счисления в другую:
  • число 39 из десятичной системы счисления в 2-ную
  • число 11001100 из двоичной системы счисления в 10-ную
  • число DBC из шестнадцатеричной системы счисления в 3-ную
 
  1. Выполнить действия в двоичной системе счисления:
  • 1011 + 10111
  • 10111 – 1111
  • 1100101*101
  1. Перевести из одной системы счисления в другую:
  • число 89 из десятичной системы счисления в 2-ную
  • число 110100101 из двоичной системы счисления в 10-ную
  • число 110111 из двоичной системы счисления в 6-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 10011 + 1101 · 11000 – 1101 · 1011*111
  1. Перевести из одной системы счисления в другую:
  • число 73 из десятичной системы счисления в 2-ную
  • число 1110011 из двоичной системы счисления в 10-ную
  • число 111101 из двоичной системы счисления в 7-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 11001 – 10101 · 10011 * 111 · 11001 + 100011
  1. Перевести из одной системы счисления в другую:
· число 64 из десятичной системы счисления в 2-ную · число 111100101 из двоичной системы счисления в 10-ную · число 100101 из двоичной системы счисления в 5-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 11011 + 11111 · 11101 – 1101 · 1011*1001
  1. Перевести из одной системы счисления в другую:
· число 71 из десятичной системы счисления в 2-ную · число 101100101 из двоичной системы счисления в 10-ную · число 111101 из двоичной системы счисления в 6-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 10111 – 1101 · 10011 * 1010 · 11011 + 11111
  1. Перевести из одной системы счисления в другую:
  • число 85 из десятичной системы счисления в 2-ную
  • число 110101 из двоичной системы счисления в 10-ную
  • число 63D из шестнадцатеричной системы счисления в 7-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 110011 – 10001 · 101101 * 1101 · 111001 + 1101
  1. Перевести из одной системы счисления в другую:
· число 42 из десятичной системы счисления в 2-ную · число 111100001 из двоичной системы счисления в 10-ную · число 4F9 из шестнадцатеричной системы счисления в 6-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 11100+10011 · 110101-11011 · 1011*1001
  1. Перевести из одной системы счисления в другую:
· число 69 из десятичной системы счисления в 2-ную · число 111100011 из двоичной системы счисления в 10-ную · число 110101 из двоичной системы счисления в 3-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 110101+10011 · 11101-1111 · 1011*1001
  1. Перевести из одной системы счисления в другую:
· число 75 из десятичной системы счисления в 2-ную · число 111100111 из двоичной системы счисления в 10-ную · число 423 из 5-ричной системы счисления в 7-ричную
 
  1. Выполнить действия в двоичной системе счисления:
· 10101+10011 · 100111-11011 · 1011*1001
  1. Перевести из одной системы счисления в другую:
· число 312 из десятичной системы счисления в 2-ную · число 111100110 из двоичной системы счисления в 10-ную · число 621 из 7-ричной системы счисления в 5-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 111101+10011 · 11111-10111 · 1011*1001
  1. Перевести из одной системы счисления в другую:
· число 251 из десятичной системы счисления в 2-ную · число 111100100 из двоичной системы счисления в 10-ную · число 3FD из 16-ричной системы счисления в 4-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 111001+10011 · 110101-11101 · 1011*1001
  1. Перевести из одной системы счисления в другую:
· число 103 из десятичной системы счисления в 2-ную · число 1111000001 из двоичной системы счисления в 10-ную · число 565 из 7-ричной системы счисления в 3-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 111001+10011 · 111101-1101 · 1011*1001
  1. Перевести из одной системы счисления в другую:
· число 149 из десятичной системы счисления в 2-ную · число 110110111 из двоичной системы счисления в 10-ную · число 332 из 4-ной системы счисления в 6-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 111001+10011 · 11011-1001 · 1011*1001
  1. Перевести из одной системы счисления в другую:
· число 107 из десятичной системы счисления в 2-ную · число 111010111 из двоичной системы счисления в 10-ную · число 110101 из двоичной системы счисления в 7-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 100101+10011 · 111101-1111 · 1011*1001
  1. Перевести из одной системы счисления в другую:
· число 143 из десятичной системы счисления в 2-ную · число 111110111 из двоичной системы счисления в 10-ную · число 201 из 7-ричной системы счисления в 3-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 100101+100011 · 11101-1011 · 1011*101
  1. Перевести из одной системы счисления в другую:
· число 65 из десятичной системы счисления в 2-ную · число 111111111 из двоичной системы счисления в 10-ную · число 813 из 9-ричной системы счисления в 4-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 110101+100011 · 110001-1101 · 1011*111
  1. Перевести из одной системы счисления в другую:
  • число 98 из десятичной системы счисления в 2-ную
  • число 111110101 из двоичной системы счисления в 10-ную
  • число 110101 из двоичной системы счисления в 7-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 111001+100011 · 110001-11101 · 111*101
  1. Перевести из одной системы счисления в другую:
  • число 155 из десятичной системы счисления в 2-ную
  • число 111100010 из двоичной системы счисления в 10-ную
  • число 442 из 6-ричной системы счисления в 5-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 111001+10011 · 111101-10011 · 1011*111
  1. Перевести из одной системы счисления в другую:
  • число 91 из десятичной системы счисления в 2-ную
  • число 110100101 из двоичной системы счисления в 10-ную
  • число 648 из 9-ричной системы счисления в 5-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 111001+10011 · 100110-11011 · 1111*1001
  1. Перевести из одной системы счисления в другую:
  • число 88 из десятичной системы счисления в 2-ную
  • число 100111101 из двоичной системы счисления в 10-ную
  • число 435 из 7-ной системы счисления в 9-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 111001+10011 · 101101-10110 · 1011*101
  1. Перевести из одной системы счисления в другую:
  • число 115 из десятичной системы счисления в 2-ную
  • число 1010101 из двоичной системы счисления в 10-ную
  • число 306 из 7-ной системы счисления в 3-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 110101+10001 · 100101-11001 · 1111*1001
  1. Перевести из одной системы счисления в другую:
  • число 106 из десятичной системы счисления в 2-ную
  • число 110101101 из двоичной системы счисления в 10-ную
  • число 110101 из двоичной системы счисления в 6-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 100101+10011 · 110001-10101 · 111*1001
  1. Перевести из одной системы счисления в другую:
  • число 59 из десятичной системы счисления в 2-ную
  • число 1101101 из двоичной системы счисления в 10-ную
  • число 340 из 7-ной системы счисления в 5-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 110101+1001 · 110011-10011 · 1011*101
  1. Перевести из одной системы счисления в другую:
  • число 157 из десятичной системы счисления в 2-ную
  • число 1001101011 из двоичной системы счисления в 16-ную
  • число 142 из 9-ной системы счисления в 7-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 101101+10011 · 110101 - 10111 · 1111*101
  1. Перевести из одной системы счисления в другую:
  • число 233 из десятичной системы счисления в 2-ную
  • число 110100111 из двоичной системы счисления в 10-ную
  • число 110101 из двоичной системы счисления в 5-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 10001 + 11011 · 110101 - 11101 · 11101*11001
  1. Перевести из одной системы счисления в другую:
  • число 131 из десятичной системы счисления в 2-ную
  • число 110101101 из двоичной системы счисления в 10-ную
  • число 351 из 7-ной системы счисления в 5-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 110101 + 10011 · 11101 - 1011 · 111 * 1001
  1. Перевести из одной системы счисления в другую:
  • число 253 из десятичной системы счисления в 2-ную
  • число 1101101101 из двоичной системы счисления в 10-ную
  • число 404 из 6-ной системы счисления в 7-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 110101 - 10011 · 101101 + 1111 · 1011*101
  1. Перевести из одной системы счисления в другую:
  • число 141 из десятичной системы счисления в 2-ную
  • число 110101111 из двоичной системы счисления в 10-ную
  • число 511 из 7-ной системы счисления в 5-ную
 
  1. Выполнить действия в двоичной системе счисления:
· 1100 * 0111 · 11001+1011 · 111101 - 10011
  1. Перевести из одной системы счисления в другую:
  • число 147 из десятичной системы счисления в 2-ную
  • число 110100101 из двоичной системы счисления в 10-ную
  • число 1101010 из двоичной системы счисления в 9-ную

 

⇐ Предыдущая234567891011Следующая ⇒


Поделиться с друзьями:

Дата добавления: 2014-12-27; Просмотров: 2194; Нарушение авторских прав?; Мы поможем в написании вашей работы!

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
studopedia.su - Студопедия (2013 - 2024) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление




Генерация страницы за: 0.008 сек.