
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тройные интегралы
|
|
|
|
Пусть функция u=f (x, y, z) определена и непрерывна в ограниченной замкнутой области T пространства Oxyz. Разобьем область T произвольным образом на n областей V 1, V 2,…, Vn, которые назовем элементарными областями. В каждой из элементарных областей произвольным образом выберем по точке 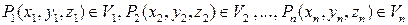 , которые назовем точками пунктуации. Обозначим через
, которые назовем точками пунктуации. Обозначим через 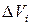 объем, а через
объем, а через  диаметр i- ойэлементарной области (i= 1,…, n),
диаметр i- ойэлементарной области (i= 1,…, n), 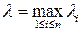 . Составим выражение
. Составим выражение
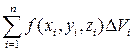 , (7)
, (7)
которое называется интегральной суммой Римана для функции u=f (x, y, z) по области T. Заметим, что выражение (7) зависит от способа разбиения области T на элементарные области и от способа выбора точек пунктуации.
Если существует предел выражения (7) при 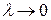 и если этот предел не зависит ни от способа разбиения области T на элементарные области, ни от способа выбора точек пунктуации, то он называется тройным интегралом от функции u=f (x, y, z) по области T и обозначается
и если этот предел не зависит ни от способа разбиения области T на элементарные области, ни от способа выбора точек пунктуации, то он называется тройным интегралом от функции u=f (x, y, z) по области T и обозначается

Таким образом,
 (8)
(8)
Свойства тройных интегралов аналогичны свойствам двойных интегралов.
Вычисление тройных интегралов сводится к вычислению повторных интегралов следующим образом. Пусть область T ограничена снизу поверхностью 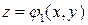 , сверху поверхностью
, сверху поверхностью 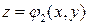 и с боков прямой цилиндрической поверхностью; проекцией области T на плоскость Oxy является область D (рис. 6). Такую область назовем правильной в направлении оси Oz.
и с боков прямой цилиндрической поверхностью; проекцией области T на плоскость Oxy является область D (рис. 6). Такую область назовем правильной в направлении оси Oz.

Рис. 6
Пусть функция u=f (x, y, z) определена и интегрируема в области T и для любых точек 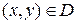 существует интеграл
существует интеграл
 .
.
Тогда существует интеграл

и справедлива формула
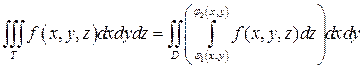 (9)
(9)
Аналогичные формулы справедливы и в случае, когда область T правильная в направлении оси Ox или оси Oy.
Теорема (о замене переменных в тройном интеграле). Пусть выполняются следующие условия:
1) функции x=x (u, v, w), y=y (u, v, w) и z=z (u, v, w) таковы, что каждой точке с координатами (x, y, z) из области T соответствует единственная точка с координатами (u, v, w) из области T 1 и наоборот;
2) функции x=x (u, v, w), y=y (u, v, w) и z=z (u, v, w) имеют непрерывные частные производные по переменным u, v и w;
3) функция u=f (x, y, z) определена и интегрируема в области T.
Тогда справедлива формула:
 , (10)
, (10)
где

- якобиан перехода от декартовых координат к криволинейным координатам.
Частным случаем криволинейных координат для тройного интеграла являются цилиндрические и сферические координаты.
1) В случае цилиндрических координат положение точки M в пространстве определяется тремя числами  , где
, где 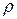 и
и  - полярные координаты проекции точки M на координатную плоскость Oxy, z – аппликата точки M (рис.7).
- полярные координаты проекции точки M на координатную плоскость Oxy, z – аппликата точки M (рис.7).

Рис. 7
Имеют место формулы:
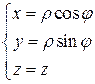 ,
,
якобиан перехода от декартовых координат к цилиндрическим равен 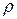 и формула (10) принимает вид:
и формула (10) принимает вид:
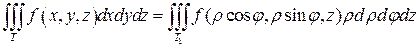 (11)
(11)
2) В случае сферических координат положение точки M в пространстве определяется тремя числами 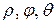 , где
, где 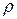 - расстояние от начала координат до точки M,
- расстояние от начала координат до точки M,  - угол между проекцией радиус-вектора точки M на плоскость Oxy и осью Ox,
- угол между проекцией радиус-вектора точки M на плоскость Oxy и осью Ox, 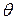 - угол между радиус-вектором точки M и осью Oz (рис.8).
- угол между радиус-вектором точки M и осью Oz (рис.8).
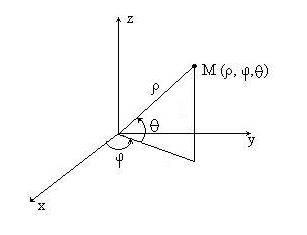
Рис. 8
Имеют место формулы:
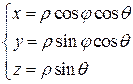 ,
,
якобиан перехода от декартовых координат к сферическим равен 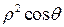 и формула (10) принимает вид:
и формула (10) принимает вид:
 (12)
(12)
Задание 1. Вычислить интеграл:

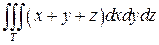 ,
,
где T - тетраэдр, ограниченный плоскостями: x+y+z =1, x= 0, y= 0, z= 0.
Решение. Изобразим область интегрирования (рис.9).
Область интегрирования ограничена снизу плоскостью z= 0, сверху плоскостью z= 1 -x-y, по бокам плоскостями x= 0 и y= 0. Проекцией области T на плоскость Oxy является область D - треугольник OAB. По формуле (9) имеем:
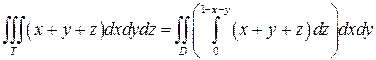 .
.
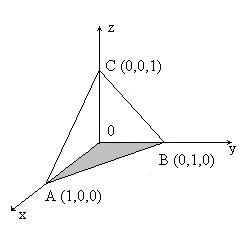
Рис. 9
Записывая двойной интеграл по области D через повторный интеграл, получим:
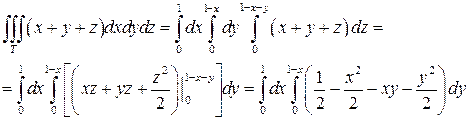
И, наконец, вычислим полученный повторный интеграл:
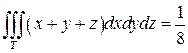 .
.
Задание 2. Перейдя к цилиндрическим координатам, вычислить интеграл:
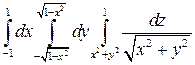 .
.
Решение. Изобразим область интегрирования (рис.10).
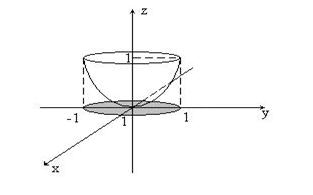
Рис. 10
Положим
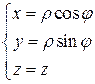
и применим формулу (11). Так как  , то
, то 
Задание 3. Переходя к сферическим координатам, вычислить интеграл:
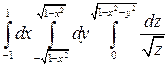 .
.
Решение. Область интегрирования T есть полушар 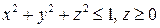 (рис.11).
(рис.11).

Рис. 11
Найдем пределы изменения сферических координат для области T 1:

Следовательно, по формуле (12) имеем:
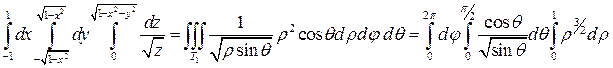 .
.
Вычислив полученный тройной интеграл, получим:
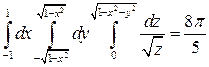 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 878; Нарушение авторских прав?; Мы поможем в написании вашей работы!