Элементы теории векторного поля

Криволинейные интегралы (2-го рода)

Приложения кратных интегралов

1. Геометрические приложения двойных интегралов

Площадь S плоской области (фигуры) D выражается в зависимости от рассматриваемой системы координат, следующими интегралами:

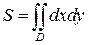(13)

- в декартовых координатах,

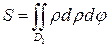(14)

- в полярных координатах.

Пусть гладкая поверхность задана уравнением z=f (x, y). Тогда площадь части этой поверхности, проектирующейся в область D плоскости O_xy, равна:

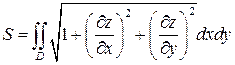(15)

Пусть область T ограничена снизу плоскостью z= 0, сверху – непрерывной поверхностью z=f (x, y) и с боков прямой цилиндрической поверхностью. Если проекцией области T на плоскость O_xy является область D, то объем V области T выражается интегралом

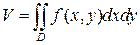(16)

2. Механические приложения двойных интегралов.

Масса M пластинки, занимающей область D плоскости O_xy, имеющей плотность , равна:

. (17)

Статические моменты M_x и M_y этойпластинки относительно осей Ox и Oy

выражаются интегралами:

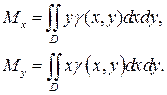(18)

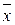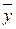Координаты центра масс и пластинки определяются следующим образом:

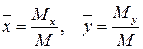. (19)

Моменты инерции пластинки относительно осей Ox и Oy соответственно равны:

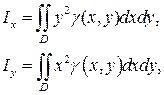(20)

а момент инерции пластинки относительно начала координат равен:

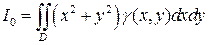. (21)

Заметим, что если рассматриваемая пластина однородна, то в приведенных формулах следует положить .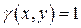

3. Геометрические приложения тройного интеграла

Объем V пространственной области T равен:

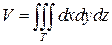(22)

4.Механические приложения тройных интегралов. Масса M тела с плотностью 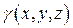,занимающего область T, равна

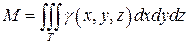(23)

Статические моменты M_xy, M_xz, M_yz тела относительно координатных плоскостей выражаются интегралами:

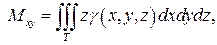
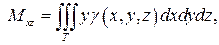(24)

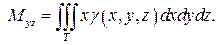
Координаты центра масс тела T определяются следующим образом:

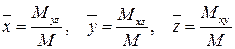. (25)

Моменты инерции тела относительно осей координат соответственно равны:

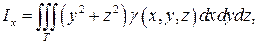
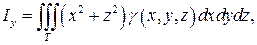(26)

.

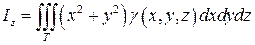Заметим, что если рассматриваемое тело однородно, то в приведенных формулах следует положить .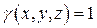

Задание 1. Найти объем тела, ограниченного поверхностями:

.

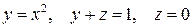Решение. Данное тело ограничено снизу плоскостью z= 0, сверху плоскостью y+z= 1 и с боков цилиндром (рис.12а).

Проекцией рассматриваемого тела является область D (рис. 12б).

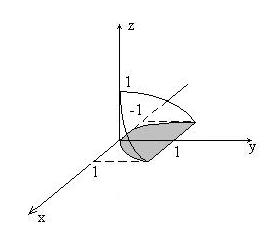
Рис. 12а

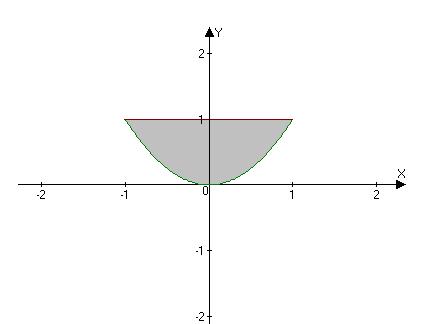
Рис. 12б

Найдем объем нашего тела двумя способами:

1) с помощью двойного интеграла;

2) с помощью тройного интеграла.

В первом случае воспользуемся формулой (16). В нашем случае f (x, y)=1 -y.

Следовательно,

.

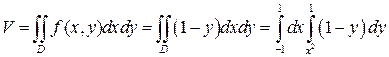Вычисляем полученный повторный интеграл:

V= 8/15.

Теперь найдем значение объема данного тела с помощью тройного интеграла. Для этого воспользуемся формулой (22). Имеем:

.

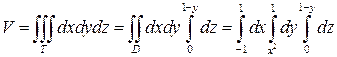Вычисляем полученный тройной интеграл:

V= 8/15.

Задание 2. Найти координаты центра масс однородного тела, ограниченного поверхностями .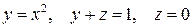

Решение. Данное тело изображено на рис.12а. Чтобы найти координаты центра масс рассматриваемого тела, воспользуемся формулами (25).

Найдем сначала массу тела. Для этого применим формулу (23) при 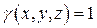, так как наше тело однородное. Имеем:

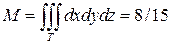
(это интеграл мы вычисляли в предыдущем примере).

Вычислим теперь статические моменты M_xy, M_xz, M_yz рассматриваемого тела относительно координатных плоскостей. Для этого воспользуемся формулами (24) при 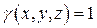. Имеем:

,

,

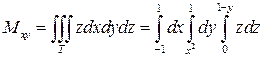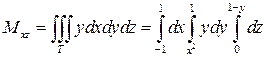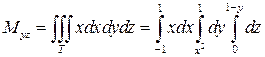
Вычислив полученные тройные интегралы, имеем:

M_xy= 16/105,

M_xz= 24/105,

M_yz= 0.

Следовательно, координаты центра масс данного тела равны:

.

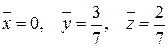Пусть функции 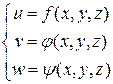определены на дуге MN кривой L. Разобьем дугу MN произвольным образом на n частей точками M=A ₀, A ₁,…, A_n = N,где A_i = A_i (x_i, y_i,z_i), i= 0,1,…, n. Полученные дуги A_{i -1} A_i, i= 1,…, n назовем элементарными дугами. В каждой из них произвольным образом выберем по точке 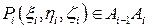, i= 1,…, n, которые назовем точками пунктуации. Введем обозначения:

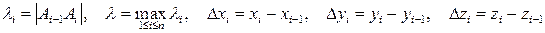
и составим выражение

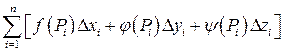, (27)

которое называется интегральной суммой Римана для данных функцийпо дуге MN. Заметим, что выражение (27) зависит от способа разбиения дуги MN на элементарные дуги и от способа выбора точек пунктуации.

Если существует предел выражения (27) при 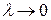и если этот предел не зависит ни от способа разбиения дуги MN на элементарные дуги, ни от способа выбора точек пунктуации, то он называется криволинейным интегралом 2-го рода по дуге MN и обозначается

.

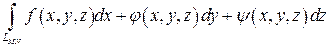Следовательно, по определению

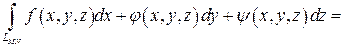
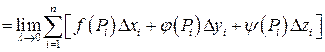(28)

Свойства криволинейных интегралов 2-го рода аналогичны свойствам определенных интегралов.

Теорема (о вычислении криволинейных интегралов 2-го рода). Пусть даны параметрические уравнения дуги MN:

,

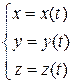где 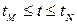и пусть функции x (t), y (t), z (t) имеют непрерывные производные. Тогда:

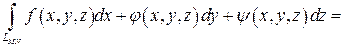(29)

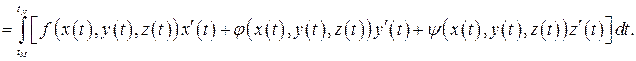
Задание 1. Вычислить интеграл

где линия L - отрезок O A с концами в точкахO(0,0,0), A (3,6,9).

Решение. Составим параметрические уравнения отрезка O A:

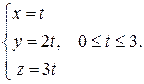
Тогда по формуле (29) имеем:

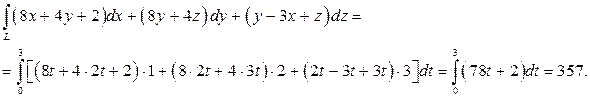
1. 5. Поверхностные интегралы (1-го рода)

Пусть функция u=f (x, y, z) определена и непрерывна на поверхности S пространства O_xyz. Разобьем поверхность S произвольным образом на n частей: S ₁, S ₂,…, S_n, которые назовем элементарными областями. В каждой из элементарных областей произвольным образом выберем по точке 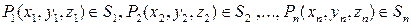, которые назовем точками пунктуации. Обозначим через 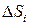, i= 1,…, n площадь i- ой элементарной области, 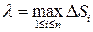. Составим выражение

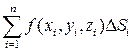, (30)

которое называется интегральной суммой Римана для функции u=f (x, y, z) по поверхности S. Заметим, что выражение (30) зависит от способа разбиения поверхности S на элементарные области и от способа выбора точек пунктуации.

Если существует предел выражения (30) при 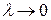и если этот предел не зависит ни от способа разбиения поверхности S на элементарные области, ни от способа выбора точек пунктуации, то он называется поверхностным интегралом 1-го рода от функции u=f (x, y, z) по поверхности S иобозначается

.

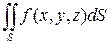Таким образом,

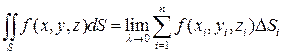(31)

Свойства поверхностных интегралов 1-го рода аналогичны свойствам двойных интегралов.

Теорема (о вычислении поверхностных интегралов 1- го рода).

Пусть поверхность S задана в явном виде уравнением 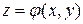, где 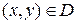, D - областьплоскости O_xy и пусть функция 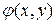имеет непрерывные частные производные первого порядка. Тогда справедлива формула:

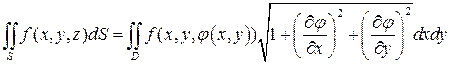(32)

Задание 1. Вычислить интеграл

,

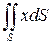где S - полусфера, задаваемая уравнением .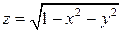

Решение. Рассматриваемая поверхность S задана в явном ви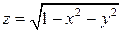де: , где 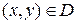- круг радиуса R= 1 (рис.11). Для вычисления данного интеграла воспользуемся формулой (32). Имеем:

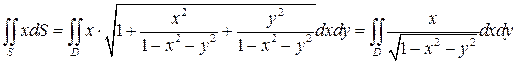
Перейдем в полученном двойном интеграле к полярной системе координат:

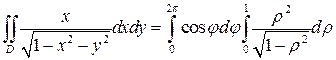
Так как значение первого интеграла 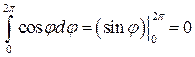, то и весь интеграл равен нулю.

Пусть в области T трехмерного пространства задано векторное поле: .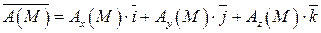

Основными операциями данногополя 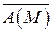являются дивергенция 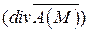и ротор 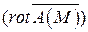. В декартовых координатах:

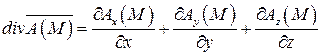, (33)

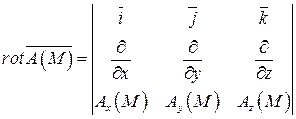(34)

Потоком векторного поля 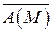через выбранную сторону поверхности S называется поверхностный интеграл 1-го рода по поверхности S от функции:

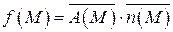
где 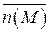- орт нормали к выбранной стороне поверхности S:

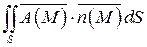(35)

ТеоремаГаусса-Остроградского (о вычислении потока векторного поля).

Пусть в некоторой замкнутой пространственной области T, ограниченной поверхностью S, задано векторное поле 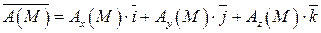, где функции A_x (M), A_y (M), A_z (M) имеют непрерывные частные производные. Тогда имеет место формула:

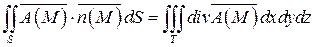(36)

Интегралом типа работы векторного поля

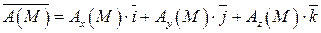
по линии L называется криволинейный интеграл 2-го рода вида:

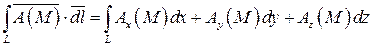(37)

Теорема Стокса (о вычислении циркуляции векторного поля).

Пусть на поверхности S и ее границе L задано векторное поле

,

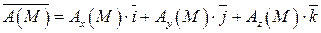где функции A_x (M), A_y (M), A_z (M) имеют непрерывные частные производные. Тогда имеет место формула:

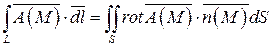, (38)

где 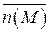- орт нормали к поверхности S, направленный так, что при обходе контура L область, ограниченная L, остается слева, если смотреть с конца орта нормали.

Задание 1. Дано векторное поле 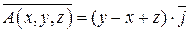и плоскость P:

2 x-y+ 2 z- 2=0, которая с координатными плоскостями образует пирамиду T. Пусть поверхность S_ABC – грань пирамиды(треугольник АВС), принадлежащая плоскости P, L_ABC - контур, ограничивающий S_ABC.

Вычислить:

1) поток векторного поля 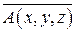через полную поверхность S пирамиды T в направлении внешней нормали (непосредственно и по теореме Гаусса-Остроградского);

2)циркуляцию данного векторного поля 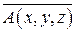по контуру L_ABC (непосредственно и по теореме Стокса).

Решение.

1) Изобразим пирамиду (рис.13).

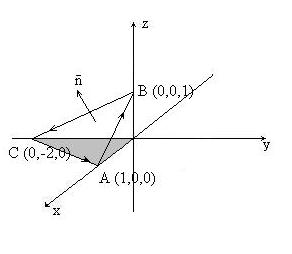
Рис. 13

Тогда поток данного векторного поля равен:

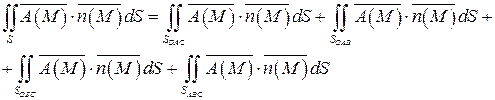
Вычислим каждый из интегралов правой части последнего равенства.

а)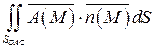

Уравнение поверхности S_OAC: z= 0 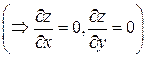; орт нормали к S_OAC имеет вид: 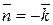; поверхность S_OAC проектируется в область D_OAC плоскости O_xy (рис. 14).

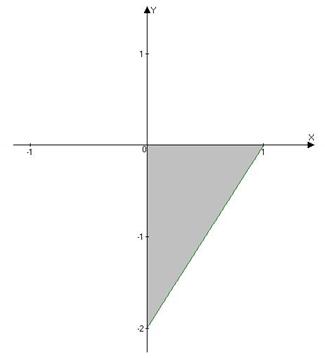
Рис. 14

Так как орт нормали к поверхности 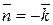, то подынтегральная функция рассматриваемого интеграла 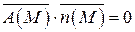. Следовательно,

.

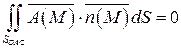б)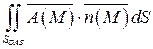

Уравнение поверхности S_OAB: y =0 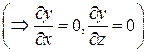; орт нормали к S_OAB имеет вид: 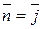; поверхность S_OAB проектируется в область D_OAB плоскости O_xz (рис.15). Следовательно, в силу формулы (32):

.

Вычислив полученный повторный интеграл, имеем:

.

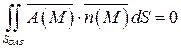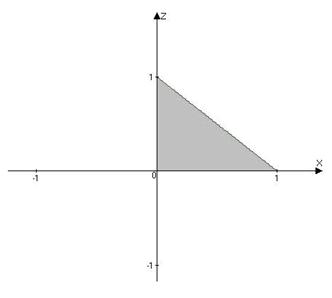
Рис. 15.

в)

Уравнение поверхности S_OBC: x =0 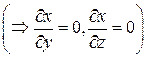; орт нормали к S_OBC имеет вид: 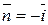; поверхность S_OBC проектируется в область D_OBC плоскости O_yz (рис.16). Так как орт нормали 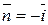, то подынтегральная функция рассматриваемого интеграла 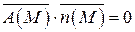. Следовательно,

.

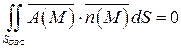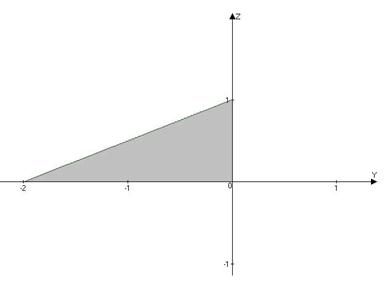
Рис. 16

г)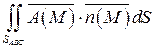

Уравнение поверхности S_ABC: 2 x - y +2 z -2=0 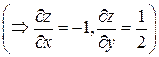; орт нормали к S_ABC имеет вид: 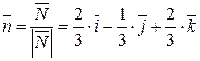; поверхность S_ABC проектируется в область D_ABC плоскости O_xy, совпадающую с областью D_OAC (рис.14). Следовательно, в силу формулы (32) имеем:

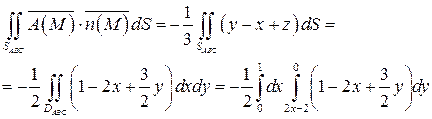
Вычислим полученный повторный интеграл:

.

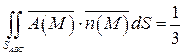Таким образом, поток векторного поля 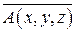через полную поверхность S данной пирамиды T равен:

.

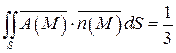2) Вычислим теперь поток данного векторного поля 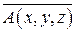через полную поверхность S пирамиды T по теореме Гаусса-Остроградского:

.

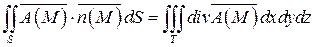Дивергенция данного векторного поля 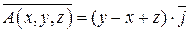равна:

.

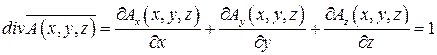Следовательно,

.

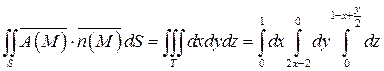Вычисляем полученный тройной интеграл:

.

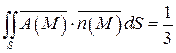Решение 2

1) Вычислим циркуляцию данного векторного поля 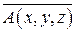по контуру L_ABC:

.

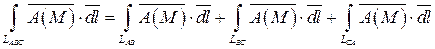Вычислим каждый из интегралов правой части полученного равенства:

а) .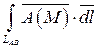

Составим параметрические уравнения отрезка AB:

,

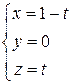где 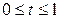. Тогда в силу формулы (29) имеем:

.

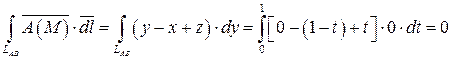б) .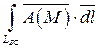

Составим параметрические уравнения отрезка BC:

,

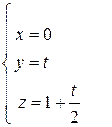где t меняется от 0 до -2. Тогда в силу формулы (29) имеем:

.

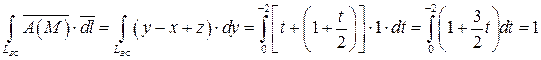в) .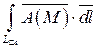

Составим параметрические уравнения отрезка CA:

,

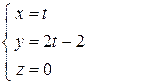где 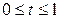. Тогда в силу формулы (29) имеем:

.

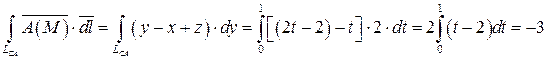Следовательно, циркуляция данного векторного поля 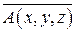по контуру L_ABC равна: .

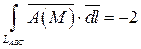2) Вычислим теперь циркуляцию векторного поля 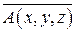по контуру L_ABC с помощью теоремы Стокса:

.

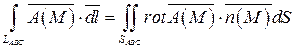Для этого найдем ротор данного векторного поля :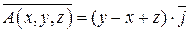

.

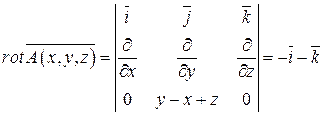Орт нормали к поверхности S_ABC мы находили при вычислении потока векторного поля 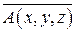: 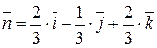(п.1а). Следовательно,

.

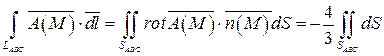Уравнение поверхности S_ABC: 2 x-y+ 2 z- 2=0 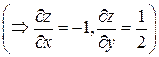; поверхность S_ABC проектируется в область D_ABC плоскости O_xy (рис.14). Таким образом, в силу формулы (32) имеем:

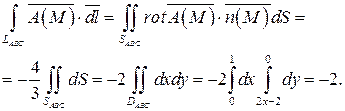
Дата добавления: 2014-12-27