Числовые ряды. Теоретические вопросы

Теоретические вопросы

Ряды

Числовые ряды. Основные понятия.

Необходимый признак сходимости числового ряда.

Признаки сравнения числовых рядов.

Признак Даламбера.

Признак Коши.

Интегральный признак Коши.

Знакопеременные ряды. Основные понятия.

Признак Лейбница.

Степенные ряды. Область сходимости степенных рядов.

Ряды Тейлора.

Ряды Фурье.

Литература

1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.

2. Щипачев В.С. Высшая математика. М.: Высш. шк., 1990.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М.: Высш. шк.,1998. Ч.1,2.

Ряд – это выражение вида

a ₁ + a ₂ + a ₃ + … + a_n + …, (1)

составленное из бесконечного множества чисел a ₁, a ₂, …, a_n, …, называемых членами ряда: a ₁ - первый член, a ₂ - второй член и т.д.; a_n называют n- ым или общим членом ряда. Ряд (1) можно сокращенно записать как 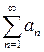. Конечные суммы вида

S ₁= a ₁,

S ₂= a ₁ + a ₂,

S ₃= a ₁ + a ₂+ a ₃,

……………………..

S_{n -1}= a ₁ + a ₂+ a ₃ + … + a_{n -1},

S_n = a₁ + a ₂+ a ₃+ … + a_{n -1} + a_n,

называются частичными суммами ряда (1):

S ₁ – первая частичная сумма, S ₂ - вторая частичная сумма, …, S_n - n- ая частичная сумма ряда (1).

Если существует конечный предел последовательности частичных сумм ряда (1) , то говорят, что этот ряд сходится, а число S называют суммой ряда (1). При этом можно писать:

a₁ + a₂ + a₃ + … + a_n + …= S.

Если же последовательность частичных сумм ряда не имеет конечного предела, то говорят, что этот ряд расходится.

k-ым остаточным рядом ряда (1)называется ряд, который получается из ряда (1) в результате отбрасывания первых k его членов:

a_k+1 + a_k+2 + a_k+3 + … + a_n + … (2)

Дата добавления: 2014-12-27