Формула Симпсона

Еще одна возможность получения квадратурных формул - использование метода Рунге-Ромберга (подраздел 3.3). Для вычисления интеграла

(16)

применим обобщенную формулу трапеций (14) с n=2

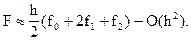(17)

на сетке с шагом h=(b-a)/2. Здесь, в соответствии с обозначениями формулы (3.13),

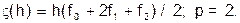(18)

На сетке с вдвое более крупным шагом 2h=b-a главная часть формулы трапеций имеет вид

(19)

Учитывая, что r=2, после применения формулы Рунге-Ромберга (3.15) получим уточненную квадратурную формулу

(20)

называемую формулой Симпсона.

Более детальный анализ позволяет определить главный член погрешности

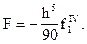(21)

Таким образом, формула Симпсона (20) имеет четвертый порядок точности. Она точна для многочлена третьей степени.

Обобщенная формула Симпсона для равномерной сетки и четного числа шагов n имеет вид

(22)

4.5. Формулы Гаусса и Маркова

Квадратурная формула Ньютона-Котеса (3) имеет n+1 параметр с_i. Поэтому она точна для полинома n-й степени. Гаусс рассматривал узловые точки x_i также как варьируемые параметры, общее число которых при этом становится равным 2(n+1). Таким образом, рациональным выбором узловых точек можно получить квадратурные формулы Гаусса, точные для полиномов (2n+1)-й степени. Эти формулы записываются для a=-1, b=1 в виде

(23)

Ниже приведены узлы и веса для формул с различным числом узлов m:

(24)

Если интеграл задан в произвольном виде, то к стандартному виду (23) он приводится заменой переменных x=kx+d, где k=(b-a)/2; d=(a+b)/2.

Границы области интегрирования часто вызывают особый интерес и поэтому бывает необходимо расположить в них узлы. Если остальные узлы выбирать из соображений наивысшей точности квадратурной формулы, то последняя, называемая формулой Маркова, будет иметь точность на два порядка меньшую, чем соответствующая формула Гаусса. Узлы и веса для квадратурных формул вида (23) имеют следующие значения:

(25)

4.6. О сходимости квадратурных формул

Обобщенные формулы средних, трапеций, Симпсона и другие формулы Ньютона-Котеса являются интегральными суммами, поэтому при n®8 они сходятся к точному значению интеграла для непрерывных подынтегральных функций. Можно также доказать аналогичные утверждения и для формул Гаусса и Маркова.

Скорость сходимости квадратурных формул связана с оценкой их остаточного члена:

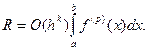(26)

Порядок точности формулы — к, но при условии, что 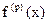— кусочно-непрерывна и ограниченна, либо неограни­ченна, но интегрируема с квадратом. Если же 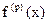не удовлетворяет этим условиям, то порядок точности будет меньшим, чем к.

Таким образом, увеличивать порядок точности применяемых квадратурных формул имеет смысл до тех пор, пока главный член погрешности (26) удовлетворяет сформулированным выше условиям. Иначе применение “более точных” формул не даст более точного результата. Повышать точность интегрирования функций малой гладкости следует за счет увеличения числа подынтервалов интегрирования.

Дата добавления: 2014-12-27