Метод прогонки

Метод Гаусса (схема единственного деления)

Методы решения СЛАУ

Все методы решения СЛАУ делят на две группы: прямые и итерационные.

Прямые методы имеют следующие отличительные особенности:

1) их погрешность равна нулю;

2) решение гарантируется после предопределенного количества вычислительных операций;

3) требуется заранее вычисленная матрица A.

Итерационные методы имеют следующие отличительные особенности:

1) их погрешность отлична от нуля;

2) решение может быть получено, если метод сходится; количество вычислительных операций заранее неизвестно и зависит от требуемой точности;

3) при вычислениях, как правило, последовательно используются отдельные уравнения и не обязательно заранее вычислять всю матрицу A.

4) алгоритм очень прост.

Идея метода состоит в приведении заданной СЛАУ к СЛАУ с треугольной матрицей (прямой ход) с последующим ее решением (обратный ход).

Прямой ход заключается в исключении поддиагональных слагаемых и начинается с того, что первое (ведущее) уравнение СЛАУ (5.1) делится на т.н. ведущий коэффициент a₁₁ = a_11,0:

. (5.9)

Затем каждое из 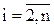уравнений делится на коэффициент, находящийся под ведущим (a_i1) и от него вычитается ведущее уравнение (9). Получается СЛАУ, состоящая из уравнения (9) и уравнений без первого столбца вида

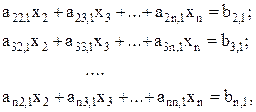(5.10)

Теперь ведущим выбирается второе уравнение СЛАУ, а ведущим коэффициентом - a_22,1. После деления ведущего уравнения на ведущий коэффициент получаем

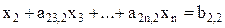. (5.11)

Затем каждое из 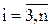уравнений делится на коэффициент, находящийся под ведущим (a_i1) и от него вычитается ведущее уравнение (5.11). Получается СЛАУ, состоящая из уравнений (5.9), (5.11) и уравнений без первых двух столбцов вида

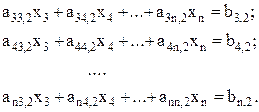(5.12)

Последовательное повторение этих операций приводит СЛАУ к виду

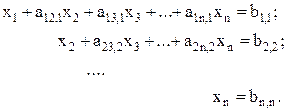(5.13)

Обратный ход - это решение СЛАУ (13), начиная с последнего уравнения.

Всего производится приблизительно 2/3n³ арифметических действий (около половины из них - сложения, столько же умножений и n делений).

Вычисление определителя матрицы A использует результаты прямого хода:

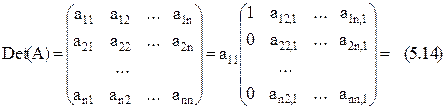
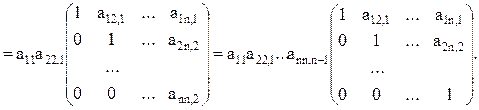
Метод Гаусса неприменим, если какой-либо ведущий коэффициент равен нулю. Также нежелательно, если ведущий коэффициент близок к нулю. Это ухудшает точность расчетов. Для избежания таких ситуаций каждый раз ведущим назначается такое уравнение, которое дает максимальный по модулю ведущий элемент (главный элемент). Это связано с перестановкой уравнений (строк матрицы A) перед этапом исключения поддиагональных элементов каждого столбца. Такая модификация метода называется методом Гаусса с выбором главного элемента по столбцу.

Вычисление определителя этим методом отличается тем, что перемена местами строк определителя изменяет его знак на противоположный:

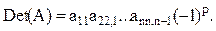(5.15)

Здесь p - количество перемен местами уравнений на этапе прямого хода.

Если матрица СЛАУ ленточная трехдиагональная, то метод Гаусса принимает более компактную форму и называется методом прогонки. СЛАУ при этом имеет следующий вид:

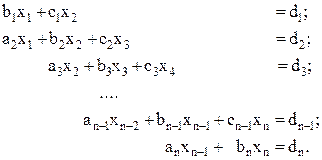(5.16)

При прямой прогонке каждое неизвестное x_i выражается через x_{i+ 1}:

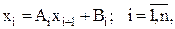(5.17)

где

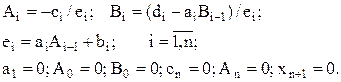(5.18)

Обратная прогонка состоит в определении всех неизвестных, начиная с последнего, по формулам (5.17) и (5.18).

Всего производится приблизительно 9/2n арифметических действий.

Если выполнено условие преобладания диагональных элементов

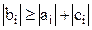, (5.19)

то в формулах прямого хода не возникнет деления на ноль.

Вычисление определителя происходит в соответствии с методом Гаусса:

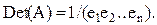(5.20)

Дата добавления: 2014-12-27