Итерационные методы решения СЛАУ

Итерационные методы решения СЛАУ заключаются в построении последовательности векторов 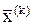(k=0,1,2,…), сходящейся к вектору - решению :

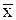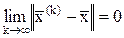. (5.40)

На практике приближенное решение считается найденным, если норма вектора невязки в (5.40) монотонно уменьшается с ростом k (метод сходится) и выполняется условие

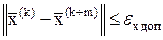, (5.41)

где 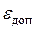- допустимая погрешность, а m достаточно велико, чтобы считать 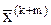"точным" по сравнению с .

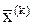Кроме условия (5.41) на практике также применяется условие малости невязки для СЛАУ:

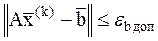. (5.42)

Различные методы различаются алгоритмами построения указанной последовательности, но все они основаны на итерационных алгоритмах вычисления, то есть алгоритмах, многократно использующих одни и те же формулы, и все они нуждаются в том, чтобы было задано начальное приближение решения .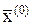

Метод простой итерации строится приведением СЛАУ (1) к виду

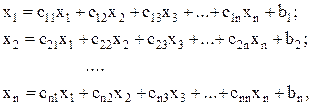(5.43)

после чего итерационный процесс принимает следующий вид:

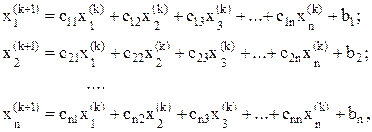(5.44)

где k = 0,1,2,….

Достаточные условия сходимости:

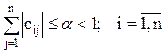(5.45)

или

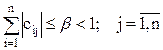. (5.46)

Оценки погрешности:

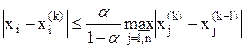, (5.47)

если выполнено условие (45) или

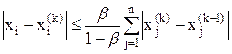, (5.48)

если выполнено условие (46).

Метод Зейделя является модификацией метода простой итерации:

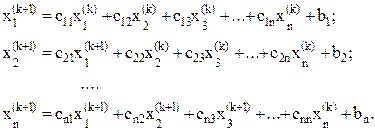(5.49)

Условия и оценки его сходимости какие же, как и для метода простой итерации. Дополнительное условие сходимости: если матрица СЛАУ симметричная положительно определенная, то метод Зейделя сходится.

В методе релаксации каждая итерация состоит из двух шагов:

1) в соответствии с методом Зейделя (49) определяется промежуточное значение вектора ;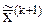

2) определяется очередное приближение вектора

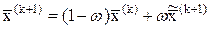. (5.50)

Здесь 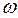- параметр релаксации, выбором которого можно влиять на свойства итерационного процесса. При 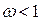имеем метод нижней релаксации, при 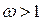- метод верхней релаксации.

Для СЛАУ с симметричной положительно определенной матрицей метод релаксации сходится при .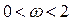

Дата добавления: 2014-12-27