
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение
|
|
|
|
.
.
Решение.
а) 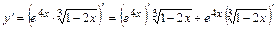 , где
, где

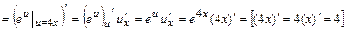 =
=  ;
; 
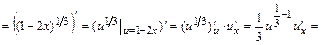


Тогда  .
.
б) 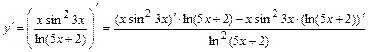 , где
, где
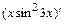
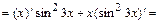
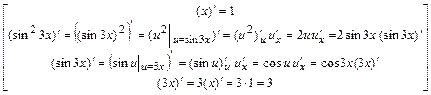
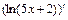


 .
.
Тогда 
в) Производную функции 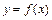 , заданной параметрическими уравнениями
, заданной параметрическими уравнениями  находим по формуле
находим по формуле  , где
, где
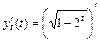
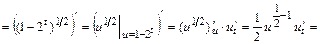
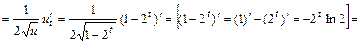
 ;
;

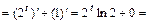
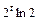 .
.
Тогда 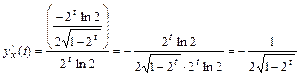 .
.
151-160. Вычислить пределы, используя правило Лопиталя.
а)  ; б)
; б) 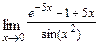 ; в)
; в) 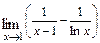 .
.
Вычисление предела  , где
, где  , всегда начинают с подстановки в
, всегда начинают с подстановки в  предельного значения её аргумента
предельного значения её аргумента 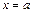 . Если в результате получают неопределённость
. Если в результате получают неопределённость 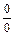 или
или  , то для её раскрытия применяют правило Лопиталя:
, то для её раскрытия применяют правило Лопиталя: 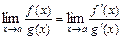 , где
, где 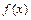 и
и  - функции, дифференцируемые в окрестности
- функции, дифференцируемые в окрестности  . В некоторых случаях может потребоваться неоднократное применение данного правила. На каждом этапе его применения следует использовать, упрощающие отношение, тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов. Раскрытие неопределённостей вида:
. В некоторых случаях может потребоваться неоднократное применение данного правила. На каждом этапе его применения следует использовать, упрощающие отношение, тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов. Раскрытие неопределённостей вида: 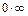 ,
,  ,
, 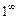 ,
,  ,
,  путём преобразований:
путём преобразований: 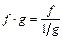 ,
,  ,
,  сводят к раскрытию неопределенностей вида
сводят к раскрытию неопределенностей вида 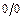 или
или  .
.
Решение.
а) 
 , где
, где
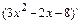

 ,
,


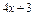
Тогда 
 .
.
б) 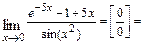
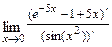 , где
, где
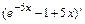
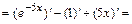
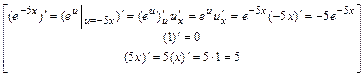
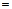
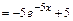 ,
,


 .
.
Тогда 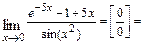
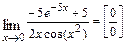 . Применяем правило Лопиталя ещё раз:
. Применяем правило Лопиталя ещё раз: 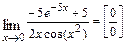
 , где
, где
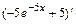

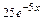 ,
,


 =
= 
 .
.
Тогда 
 .
.
в)  . Преобразуем данную неопределённость (приведением разности дробей к общему знаменателю) к виду
. Преобразуем данную неопределённость (приведением разности дробей к общему знаменателю) к виду  , после чего применим правило Лопиталя. Получим
, после чего применим правило Лопиталя. Получим 
= 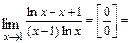
 , где
, где

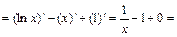
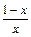 ,
,


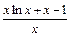 .
.
Тогда 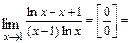
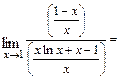
 .
.
Применяем правило Лопиталя ещё раз:

 , где
, где 

 ,
,
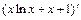
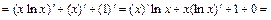

 .
.
В итоге получим 
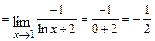 .
.
Ответ:
а)  ; б)
; б) 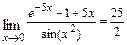 ; в)
; в)  .
.
161-170. Провести полное исследование функции 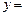
 и построить её график.
и построить её график.
Для построения графика функции 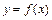 нужно:
нужно:
1) найти область определения функции;
2) найти область непрерывности функции и точки разрыва;
3) исследовать функцию на чётность, нечётность и периодичность;
4) найти точки пересечения графика с осями координат;
5) найти асимптоты графика функции;
6) найти интервалы возрастания и убывания, экстремумы функции;
7) найти интервалы выпуклости, вогнутости и точки перегиба.
1) Находим область определения функции: 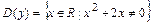 =
=  ).
).
2) Поскольку данная функция является элементарной, то областью её непрерывности является область определения 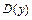 , а точками разрыва являются точки
, а точками разрыва являются точки  и
и 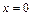 , не принадлежащие множеству
, не принадлежащие множеству 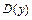 , но являющиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва в точках
, но являющиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва в точках  и
и 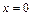 , вычислив в них односторонние пределы функции:
, вычислив в них односторонние пределы функции:
 ,
,  ,
,
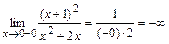 ,
,  .
.
Так как односторонние пределы функции в точках  и
и 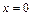 - бесконечные, то данные точки являются точками бесконечного разрыва.
- бесконечные, то данные точки являются точками бесконечного разрыва.
3) Функция не является периодической.
Функция 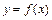 , в аналитическое выражение которой входит хотя бы одна непериодическая функция периодической не является.
, в аналитическое выражение которой входит хотя бы одна непериодическая функция периодической не является.
Проверяем является ли функция чётной или нечётной. Так как область определения функции 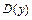 =
=  ) не симметрична относительно точки
) не симметрична относительно точки 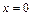 , то данная функция – общего вида.
, то данная функция – общего вида.
4) Находим точки пересечения графика с осями координат.
Так как  , то точек пересечения графика с осью
, то точек пересечения графика с осью  нет.
нет.
Положим 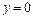 и решим уравнение
и решим уравнение 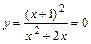 . Его решением является
. Его решением является  . Следовательно, точка
. Следовательно, точка  - точка пересечения графика с осью
- точка пересечения графика с осью 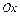 .
.
5) Находим вертикальные и наклонные асимптоты графика функции.
Прямая 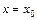 является вертикальной асимптотой, тогда и только тогда, когда
является вертикальной асимптотой, тогда и только тогда, когда 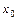 является точкой бесконечного разрыва функции
является точкой бесконечного разрыва функции 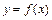 .
.
Так как точки  и
и 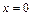 - точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямые
- точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямые  и
и 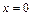 .
.
Прямая 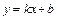 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 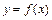 при
при  тогда и только тогда, когда одновременно существуют конечные пределы:
тогда и только тогда, когда одновременно существуют конечные пределы:  и
и 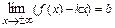 .
.
Вычисляем сначала пределы при 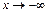 :
:
 ,
,  .
.
В дальнейшем будем иметь в виду следующий часто встречающийся предел: 
Следовательно 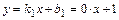 , т.е.
, т.е. 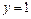 - наклонная (горизонтальная) асимптота графика функции при
- наклонная (горизонтальная) асимптота графика функции при 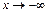 .
.
Аналогично вычисляем пределы при  :
:  ,
,  Следовательно
Следовательно  , т.е.
, т.е. 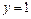 - наклонная (горизонтальная) асимптота графика функции при
- наклонная (горизонтальная) асимптота графика функции при  .
.
6) Определяем интервалы возрастания, убывания, экстремумы функции. Для этого находим первую производную функции:



и определяем критические точки функции 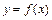 , т.е. точки
, т.е. точки  в которых
в которых 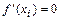 или
или 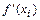 не существует:
не существует:

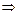
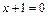
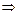
 ;
;
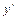 не существует при
не существует при 
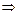
 и
и 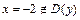 .
.
Таким образом, единственной критической (стационарной) точкой функции 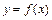 является точка
является точка  .
.
Исследуем знак производной 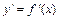 в интервалах, на которые критические точки функции
в интервалах, на которые критические точки функции 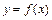 разбивают её область определения
разбивают её область определения 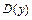 , и найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:
, и найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:
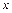
| 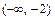
| 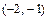
| 
| 
| 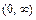
|
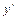
| + | + | 
| 
| 
|

| возрастает | возрастает | 
| убывает | убывает |
Так как при переходе слева направо через точку  производная
производная  меняет знак с «+» на «
меняет знак с «+» на « », то точка
», то точка  является точкой локального максимума и
является точкой локального максимума и 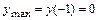 .
.
7) Определяем интервалы выпуклости, вогнутости, точки перегиба графика функции. Для этого находим вторую производную функции:


и определяем точки возможного перегиба 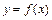 , т.е. точки
, т.е. точки  в которых
в которых  или
или  не существует:
не существует:  , так как
, так как  (квадратное уравнение не имеет действительных корней);
(квадратное уравнение не имеет действительных корней); 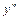 не существует при
не существует при 
 и
и 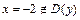 .
.
Таким образом, функция 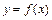 не имеет точек возможного перегиба.
не имеет точек возможного перегиба.
Исследуем знак второй производной  в интервалах, на которые точки возможного перегиба функции
в интервалах, на которые точки возможного перегиба функции 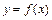 разбивают её область определения
разбивают её область определения 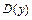 , и найдём интервалы выпуклости, вогнутости, точки перегиба графика функции. Результаты исследования представим таблицей:
, и найдём интервалы выпуклости, вогнутости, точки перегиба графика функции. Результаты исследования представим таблицей:
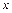
| 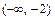
| 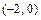
| 
|
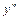
| + | 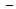
| + |

| график вогнутый | график выпуклый | график вогнутый |
Точек перегиба нет.
8) На основании полученных результатов строим график функции (рис.6)

Рис.6.
171-180. Найти наибольшее и наименьшее значения функции 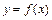 на отрезке
на отрезке 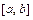 :
: 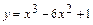 ,
, 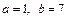 .
.
Наибольшее и наименьшее значения функции 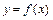 непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке
непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке  достигается или в точках
достигается или в точках  , в которых
, в которых 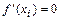 или
или 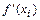 не существует, или на концах отрезка.
не существует, или на концах отрезка.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 403; Нарушение авторских прав?; Мы поможем в написании вашей работы!