Решение. 1)Находим первую производную функции:

Решение.

1) Находим первую производную функции:

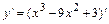
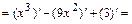
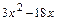
и определяем внутренние критические точки функции 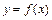, т.е. точки 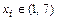в которых 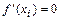или 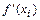не существует:

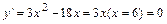
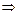
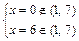, точек 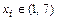в которых 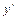не существует нет. Таким образом, единственной внутренней критической (стационарной) точкой функции 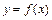на отрезке 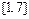является точка .

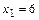2) Вычисляем значения функции 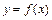во внутренних критических точках и на концах отрезка : , , .

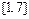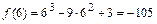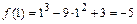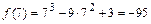3) Сравниваем значения 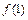, , 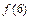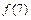и находим наименьшее и наибольшее значения функции 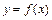на отрезке :

, .

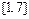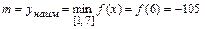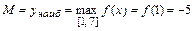Ответ: , .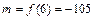

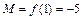181-190. Составить уравнения касательной и нормали к графику функции 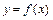в точке : , .

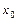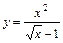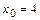Уравнение касательной к графику функции 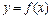в точке 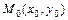имеет вид: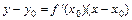

Уравнение нормали к графику функции 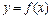в точке 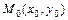имеет вид: .

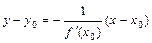1) Вычисляем значение функции 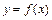в точке : .

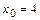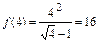2) Находим первую производную функции: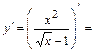

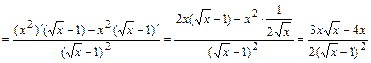и вычисляем её значение в точке : .

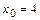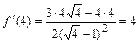3) Составляем уравнение касательной: 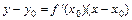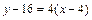изаписываем его в виде : .

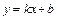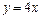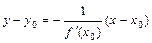
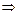
4) Составляем уравнение нормали: 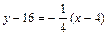изаписываем его в виде : .

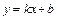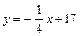Если 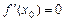, то уравнение нормали записывается в виде: .

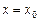Ответ: 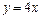- уравнение касательной; 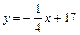- уравнение нормали.

191–200. Затраты, необходимые для производства 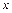единиц данной продукции задаётся функцией издержек 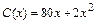. Продукция реализуется по фиксированной цене 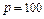(ден.ед.) за единицу продукции. Требуется найти: а) оптимальное значение 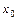выпуска продукции, при котором производитель получит максимальную прибыль; б) средние значения издержек производства и прибыли при 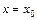; в) эластичностьиздержек производства и прибылипри 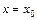. Сделать выводы.

Прибыль, получаемая производителем при выпуске 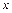единиц данной продукции, задаётся функцией 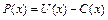, где 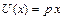- выручка от реализации 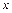единиц данной продукции по фиксированной цене 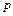(ден.ед.) за единицу продукции, 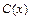-функция издержек.

Средними издержками называют величину 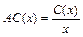(издержки в расчёте на 1 ед. выпускаемой продукции), а средней прибылью – величину 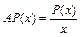(прибыль в расчёте на 1 ед. выпускаемой продукции).

Эластичностью издержек называют величину 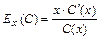(показывает приближённый процентный прирост издержек 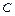при изменении 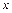на 1%), а эластичностью прибыли – 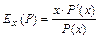(показывает приближённый процентный прирост прибыли 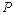при изменении 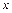на 1%).

Дата добавления: 2014-12-27