Сложные проценты

Когда-то одного из самых богатых банкиров мира барона Ротшильда попросили перечислить семь чудес света. Он ответил, что не сможет этого сделать, но зато точно знает, что существует восьмое чудо света, которым может пользоваться каждый из нас, чтобы достичь желаемого. Это чудо – сложные проценты.

В табл. 1 показан впечатляющий рост скромной стартовой суммы в 100 руб., когда на нее начисляются сложные проценты.

Таблица 1

Наращение 100 руб. по сложным процентам (руб.)

Период начисления, лет	Годовая процентная ставка
10 %	15 %	18 %	20 %
	259,4 672,7 1 744,9 4 525,9 11 739,1	404,6 1 636,7 6 621,2 26 786,4 108 356,7	523,4 2 739,3 14 337,1 75 037,8 392 735,7	619,2 3 833,8 23 737,6 146 977,2 910 043,8

Сложные проценты находят применение не только в банковских операциях, но и в бизнесе, и в государственном планировании, в частности, для оценки роста экономики, в проведении сравнительного анализа и во многих других случаях.

Как показано в следующем примере, сложные проценты – это те же простые проценты, применяемые снова и снова к сумме, которая увеличивается за счет присоединения простых процентов.

Можно сказать, что для сложных процентов характерен эффект «снежного кома».

Предположим, что инвестиции в 100 тыс. руб. вложены в дело, приносящий ежегодный 12 % доход. В случае простых процентов, годовая величина дохода составит 12 тыс. руб., а за три года 36 тыс. руб. Однако, если полученный доход не изымать, а присоединять к первоначальным инвестициям, они вырастут больше, чем на 36 тыс. руб. Рассмотрим этот случай:

первоначальные инвестиции 100 тыс. руб.

проценты за 1^ый год (12 %) 12 тыс. руб.

итого сумма на начало 2^го года 112 тыс. руб.

проценты за 2^ой год (12 %) 13,44 тыс. руб.

итого сумма на начало 3^го года 125,44 тыс. руб.

проценты за 3^ий год (12 %) 15,05 тыс. руб.

всего наращенная сумма к концу 3^го года 140,49 тыс. руб.

Таким образом, за один и тот же период (3 года), при одинаковой процентной ставке (12 %) на одну и ту же первоначальную сумму начислены разные проценты: простые – 36 тыс. руб., сложные – 40,49 тыс. руб.

В сложных процентах процентные деньги в каждом расчетном периоде присоединяются к капиталу предыдущего периода, и проценты в последующем периоде начисляются на наращенный капитал. Иногда этот способ называют начислением «процентов на проценты».

Для большого периода начислений будет утомительным расчет будущей суммы выше приведенным способом. К счастью, легко вывести формулу, позволяющую найти наращенную сумму по сложным процентам без промежуточных начислений.

К концу первого года наращенная сумма равна:

S₁ = P ( 1 + i),

где ( 1 + i) – ежегодный коэффициент наращения.

К концу второго года снова начисляются годовые проценты, но уже на наращенную сумму S₁:

S₂ = S₁ ( 1 + i) = P ( 1 + i) ( 1 + i) = Р ( 1 + i)².

Продолжив расчеты для n периодов, можно вывести формулу:

S = P ( 1 + i)ⁿ (14)

Выражение ( 1 + i)ⁿ представляет собой коэффициент наращения по сложным процентам. Его расчет не представляет особой трудности, если пользоваться специальными таблицами (прил. 2).

Пример 13.

Определить будущую сумму 60 тыс. руб., вложенную под 15 % на 10 лет.

Решение.

Воспользуемся формулой (14) и табл. 3 прил. 2: S = 60 (1 + 0,15)^10.

По таблице на пересечении колонок «15 %» и «10 лет» находим коэффициент наращения k_н = 4,046. Отсюда S = 60 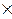4,046 = 242,76 тыс. руб.

Для нахождения первоначальной суммы следует продисконтировать наращенную сумму:

Р = 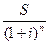; или P = S 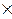k_д (15)

Коэффициент дисконтирования по сложным процентам k_д = 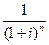можно также найти табличным способом (прил. 2).

Пример 14.

Определим первоначальную величину суммы в 10 млн руб., выплачиваемый через 3 года при сложном начислении процентов 18 % годовых.

Решение.

Воспользуемся формулой (15) и табл. 2 прил. 2. По таблице находим коэффициент дисконтирования k_д = 0,593. Отсюда Р = 10 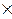0,593 = 5,93 млн руб.

До сих пор мы имели дело с ежегодным начислением процентов. Однако они могут начисляться чаще. Различают полугодовое, квартальное ежемесячное, ежедневное и даже непрерывное начисление процентов. Здесь речь идет об интервалах начисления процентов в течение года. Так, полугодовое начисление процентов означает, что они начисляются 2 раза в течение года, квартальные – 4 раза, ежемесячные – 12 раз и т.д.

Обозначим число интервалов символом m. Тогда на каждом интервале процентная ставка будет равна 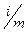. Например, если годовая процентная ставка равна 12 %, то на каждом интервале полугодового начисления ставка будет равна 6 % (12 %: 2).

Годовая процентная ставка, на основе которой определяются ставки, применяемые для различных интервалов начисления, называется номинальной и обозначается символом j.

Пример 15.

Вкладчик положил на счет в банке 50 тыс. руб. Банк начисляет проценты ежеквартально. Какая сумма будет на счете через 3 года, если номинальная процентная ставка 12 % годовых?

Решение.

За 3 года проценты будут начисляться 12 раз (3 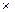4). Процентная ставка на каждом интервале начисления будет равна 3 % (12 %: 4). Следовательно, наращенная сумма составит: S = 50 (1 + 0,03)¹² = 50 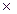1,4258 = 71,29 тыс. руб.

В этой задаче мы практически вывели формулу сложных процентов для нескольких интервалов начислений в году:

S = P ( 1 + 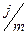)^mn (16)

Если необходимо найти исходную сумму, зная ее наращенное значение, следует воспользоваться операцией дисконтирования:

P = 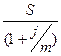_mn. (17)

Коэффициенты наращения (1 + 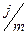)^mn и дисконтирования 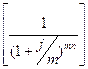легко найти по табл. 1 и 2 прил. 2.

Пример 16.

Заемщик имеет два долга:

а) 100 тыс. руб., срок погашения 3 года, процентная ставка 12 %, начисление ежеквартальное;

б) 50 тыс. руб., срок погашения 5 лет, процентная ставка 10 %, начисление полугодовое.

Он хочет погасить оба долга одновременно через 6 лет. Кредитор согласен, но с условием, что процентная ставка пролонгации долга будет равна 14 %, начисление процентов годовое. Какой величины будет платеж?

Решение.

Поскольку в условии задачи даны разновременные суммы, их сначала надо привести к одной точке во времени, а затем сложить. За базу локализации^* целесообразно принять точку «6 лет».

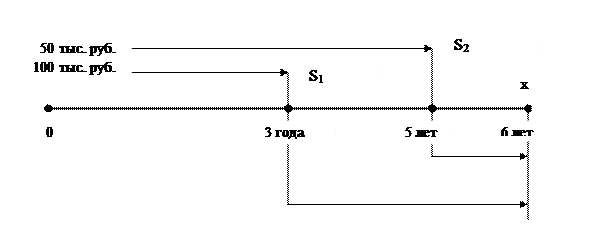
Рис. 10. Временная диаграмма примера 16

Поскольку обе суммы надо сначала нарастить, используем формулу (16).

S₁ = 100 (1 + 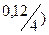^{4 3} = 100 1, 4258 = 142,58 тыс. руб.;

S₂ = 50 (1 + 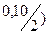^{2 5} = 50 1, 6289 = 81,45 тыс. руб.;

Зная наращенные суммы в точках «3 года» и «5 лет», приводим их к точке «6 лет», но используем процентную ставку равную 14 %.

х = S₁ (1 + 0,14)³ + S₂ (1 + 0,14)¹ = 142,58 1,4815 + 81,45 1,14 =

= 211,23 + 92,85 = 304,08 тыс. руб.

Через 6 лет заемщик погасит оба долга одним платежом 304,08 тыс. руб.

Пример 17.

5 августа 2000 г. господин N занял 60 тыс. руб. господину К под 10 %, начисляемых по полугодиям. Господин К дал долговую расписку, в которой он обязуется выплатить долг с процентами через 6 лет. Но 5 февраля 2004 г. господин N продал это обязательство фирме, которая в данной сделке применила для дисконтирования ставку в 12 % так же с полугодовым начислением. Какую сумму получил господин N?

Решение.

Построим временную диаграмму.

Рис. 11. Временная диаграмма примера 17

Сначала определим сумму, которую должен был вернуть заемщик через 6 лет, т.е. 5 августа 2006 г. Воспользуемся формулой (16):

S = 60 (1 + 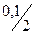)^{6 2} = 60 1,796 = 107,76 тыс. руб.

Затем эту сумму продисконтируем (17) на период между датой погашения (05.08.2006) и датой продажи обязательства (05.02.2004). Этот период составит 2,5 года. Учитывая, что начисление процентов полугодовое, количество интервалов будет равно 5 (2,5 2).

х = 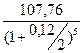= 107,76 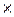0,746 = 80,39 тыс. руб.

Коэффициент наращения (1 + 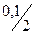)^{6 2} найден по табл. 1 прил. 2 для процентной ставки 5 % (10 %: 2) и 12 интервалов начисления (6 2). Аналогично найден коэффициент дисконтирования 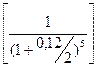по табл. 2 прил. 2.

Особым случаем сложных процентов является их непрерывное начисление, когда количество интервалов стремится к бесконечности. Это означает, что деньги растут не дискретно, а бесперебойно. На первый взгляд такая ситуация выглядит странно непривычно, но в жизни мы с ней часто сталкиваемся. Стопа человека, к примеру, с момента рождения до определенного периода формируется незримо, но непрерывно, хотя и необязательно одинаковыми темпами.

При непрерывном начислении процентов для наращеной суммы справедливо следующее выражение:

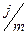S = P lim ( 1 + )^mn.

^m→∞

После преобразований эта формула принимает окончательный вид:

S = P ℮^jn, (18)

где ℮ - основание натурального логарифма (℮ = 2,71828).

Очевидно, что непрерывный способ начисления процентов дает максимальную величину наращенной суммы при прочих равных условиях, т.е. при одинаковом значении параметров P, j, n.

Пример 18. Определить наращенную сумму через 5 лет, если первоначальный капитал равен 200 тыс. руб., номинальная процентная ставка – 20 %, проценты начисляются непрерывно.

Решение.

Воспользуемся формулой (18): S = 200 (2.71828) ^{0,2 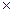5} = 543,66 тыс. руб.

Итак, наращение денег может быть 1 раз в год по ставке i или m раз в год по ставке 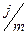. Годовая ставка i, при которой финансовый результат будет таким же как и при начислении процентов m раз в году по ставке 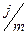, называется эффективной ставкой (i_{эф .}).

Иными словами, эффективная ставка – это годовая ставка эквивалентная номинальной ставке.

Для вышесказанного справедливо следующее выражение:

(1 + i_эф.)ⁿ = (1 + 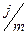)^mn,

где i_эф – эффективная годовая ставка;

j - номинальная годовая ставка.

После преобразования выражения получаем:

i_эф = (1 + 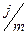)^m – 1 (19)

По этой формуле можно рассчитать эффективную ставку эквивалентную данной номинальной ставке.

Пример 19.

Определить эффективную ставку эквивалентную ставке в 8 %, начисляемых по полугодиям.

Решение.

Подставляя данные задачи в формулу (19), находим, что

i_эф = (1 + 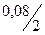)² – 1 = 0,0816 или 8,16 %.

Это значит, что наращенная сумма при ставке в 8 % с полугодовым начислением будет такой же по величине, что и наращенная сумма, полученная при ставке в 8,16 % с начислением процентов 1 раз в год.

До сих пор в примерах мы использовали формулу сложных процентов для целого числа лет (n) или интервалов (mn) начисления. В случае нецелого числа этого параметра на практике применяют смешанный метод, когда на целую часть периода начисляют сложные проценты, а на его дробную часть – простые проценты.

Тогда формула (16) примет следующий вид:

S = P (1 + 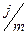) ^am (1 + j b), (20)

где а – целое число лет,

b – дробная часть года.

Пример 20.

На 60 тыс. руб. начисляются 4 %. Какой будет наращенная сумма через 3 года и 5 месяцев, если начисление процентов полугодовое?

Решение.

В течение 3^х лет проценты начисляются 6 раз (3 2) по формуле сложных процентов, в течение следующих 5^ти месяцев начисляются простые проценты.

S = 60 (1 + 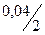)^{3 2} (1 + 0,04 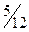) = 60 1,1262 1,0167 = 68,7 тыс. руб.

Рис. 12. Временна диаграмма примера 20

Задания для самоподготовки

Вопросы

1. Чем отличаются сложные и простые проценты?

2. Что представляет собой коэффициент наращения по сложным процентам?

3. Что представляет собой коэффициент дисконтирования в сложных процентах?

4. Какая существует связь между коэффициентами наращения и дисконтирования?

5. Что представляет собой номинальная процентная ставка?

6. Что такое эффективная процентная ставка?

7. Какая процентная ставка (сложная или простая) дает большую наращенную сумму и почему?

8. Какими бывают интервалы начисления?

9. Каким образом преобразуется формула сложных процентов, если их начисление происходит «m» раз в году?

10. В чем особенность непрерывного начисления процентов?

Задачи

Задача 1. Определить наращенную сумму, если 1 млн руб. инвестируется на 10 лет под 10 %?

(Ответ: 2593,7 тыс. руб.)

Задача 2. В день рождения сына отец положил на открытый на его имя счет 10 тыс. руб. под 8 %, начисляемых по полугодиям. Какую сумму сможет получить сын ко дню своего 18-летия?

(Ответ: 41,4 тыс. руб.)

Задача 3. Чему равна эффективная ставка эквивалентная 10 % - ной, начисляемой: а) по полугодиям; б) ежеквартально?

(Ответ: 10,25 %, 10,38 %)

Задача 4. Определить первоначальную сумму денег, положенную на счет в банке на 3 года и 8 месяцев под 6% с полугодовым начислением, если наращенная сумма составила 30 тыс. руб.?

(Ответ: 24,15 тыс. руб.)

Задача 5. На счет положено 75 тыс. руб. на 6 лет под 8 % с ежеквартальным начислением. Но через 2 года со счета списано 15 тыс. руб. Какая сумма будет на счете к концу 6-летнего периода?

(Ответ: 100,05 тыс. руб.)

Задача 6. Какой должна быть годовая процентная ставка (сложная), чтобы первоначальный капитал удвоился за 9 лет?

(Ответ: 8 %)

Задача 7. Вместо того, чтобы получить от страховой компании 1 млн руб. сейчас бенефициарий предпочел получить свой доход тремя равными годовыми платежами, первый из которых – сейчас. Страховая компания начисляет 10 %. Какова величина каждого платежа?

(Ответ: 365,63 тыс. руб.)

Задача 8. В завещании указано, что сумма в 3 млн руб., положенная на счет под 8 % с полугодовым начислением, должна быть разделена поровну между тремя детьми при достижении каждым из них 21^го–летнего возраста. Когда завещание вступило в силу, возраст детей был 19, 16 и 14 лет соответственно. Рассчитайте величину наследства, полученную каждым наследником.

(Ответ: 1423,15 тыс. руб.)

Задача 9. Чему были равны ежегодные темпы роста, если известно, что капитал в 141,1 млн руб. увеличился за период с 2000 по 2006 год до 170,3 млн руб.?

(Ответ: 3,2 %)

Дата добавления: 2014-12-27