
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аннуитеты
|
|
|
|
Когда люди делают дорогую покупку (например, квартиру, машину), они, как правило, берут ссуду в банке, а затем погашают ее ежемесячными платежами в течение нескольких лет. И весьма непросто рассчитать проценты, т.к. их количество будет, к примеру, 120, если ссуда взята на 10 лет. К счастью, выведены необходимые формулы, применение которых облегчает решение проблемы. Эта серия равновеликих ежемесячных платежей, которые выплачивает заемщик, купивший, например, квартиру, и представляет собой аннуитет или финансовую ренту.
Проценты по облигациям, страховые премии, оплата покупок частями – наиболее известные примеры аннуитетов.
Итак, серия равновеликих платежей, осуществляемых через равные промежутки времени, формирует аннуитет.
Различают определенные и неопределенные аннуитеты.
В определенных аннуитетах выплата платежей начинается и заканчивается в точно установленное время. Т.е. точно известно, когда будет выплачен первый платеж и погашен последний.
Если даты первого или последнего (или обоих) платежа не известны, то речь идет о неопределенном аннуитете. Примерами применения таких аннуитетов являются страхование жизни, пенсионное обеспечение.
Интервалы между платежами также могут быть разными: ежегодными, полугодовыми, квартальными, ежемесячными или другой фиксированный интервал.
Другое существенное различие аннуитетов – время платежей, их можно проводить как в конце каждого интервала, так и в начале. В расчетах такие аннуитеты будут различаться коэффициентами наращения и дисконтирования.
Если платежи проводятся в конце каждого интервала, то речь идет об обыкновенном аннуитете, если в начале каждого интервала, то это срочный аннуитет.
Рассмотрим подробно определенный аннуитет, платежи по которому осуществляются в конце каждого года.
Будущая, или наращенная величина аннуитета представляет собой сумму всех периодических платежей с начисленными на них процентами, накопленную к концу указанного срока, или к дате последнего платежа.
Пример 21.
На депозитный счет в конце каждого года перечисляются 5000 руб., на которые начисляются 12 %. Какая сумма будет накоплена на счете к концу 4го года?
Решение.
Понять проблемы аннуитета визуально помогает временная диаграмма. В данной задаче за точку локализации примем «4 года», именно к концу этого года на счете будет накоплена искомая сумма.
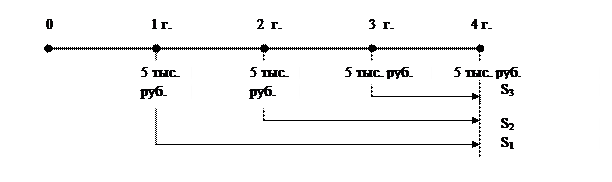
Рис. 13. Временная диаграмма примера 21 
По формуле (14) рассчитаем наращенную величину каждого платежа:
для первого платежа S1 = 5 (1 + 0,12)3 = 5  1,405 = 7,025 тыс. руб.
1,405 = 7,025 тыс. руб.
для второго платежа S2 = 5 (1 + 0,12)2 = 5  1,254 = 6,27 тыс. руб.
1,254 = 6,27 тыс. руб.
для третьего платежа S3 = 5 (1 + 0,12)1 = 5  1,120 = 5,60 тыс. руб.
1,120 = 5,60 тыс. руб.
для четвертого платежа S4 = 5 тыс. руб.
Итого к концу 4го года на счете будет накоплено: 7,025 + 6,27 + 5,60 + 5 = = 23,895 тыс. руб.
Обратите внимание, что наращенная сумма последнего платежа равна самому платежу, поскольку нет времени (оно равно нулю) для начисления процентов.
Если количество платежей невелико, расчет можно осуществлять по выше приведенной схеме, находя наращенные суммы каждого платежа и суммируя их. Но если платежей много, то такой способ расчета будет достаточно тяжелым.
На практике пользуются формулой:
Sоб. = R 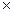
 = R
= R 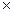 k
k 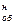 (21)
(21)
где Sоб. – наращенная или будущая величина обыкновенного аннуитета;
R – периодический платеж;
i – годовая процентная ставка (относительная величина);
n – количество платежей.
Выражение в квадратных скобках представляет собой коэффициент наращения аннуитета. Его значение легко найти по табл. 3 прил. 2.
По условиям выше приведенного примера найдем наращенную величину аннуитета, воспользовавшись формулой (20) и табл. 3 прил. 2:
Sоб . = 5 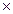 4,779 = 23,895 тыс. руб.
4,779 = 23,895 тыс. руб.
Результат такой же, но расчет намного проще.
Зная наращенную сумму аннуитета, можно вычислить величину периодического платежа:
R = Sоб. 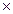
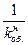 (21)
(21)
где k 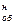 - коэффициент наращения обыкновенного аннуитета.
- коэффициент наращения обыкновенного аннуитета.
Пример 22.
Чтобы накопить за 5 лет 100 тыс. руб., какую сумму необходимо перечислять на счет, если банк начисляет 10 %?
Решение.
Известна будущая величина аннуитета. По табл. 3 прил. 2 найдем коэффициент наращения аннуитета для n = 5 и i = 10 %.
k 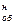 = 6,105
= 6,105
Тогда R = 100. 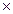
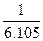 = 16,38 тыс. руб.
= 16,38 тыс. руб.
Мы рассмотрели будущую величину аннуитета, как сумму всех наращенных платежей к моменту совершения последнего платежа. Но бывает ситуация, когда после завершения всех платежей накопленная сумма продолжает приносить проценты.
Пример 23.
Платежи в размере 3 тыс. руб. поступают на накопительный счет каждые полгода в течение 3 лет. На них начисляются проценты по ставке 8 %. После того, как сделан последний платеж, деньги остаются на счете еще 2 года. Найти наращенную сумму.
Решение.
Известна величина платежей, число которых равно 6 (3 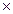 2), на каждом полугодовом интервале начисляются 4 % (8: 2). К концу 3го года на счете будет сумма: Sоб = 3
2), на каждом полугодовом интервале начисляются 4 % (8: 2). К концу 3го года на счете будет сумма: Sоб = 3 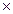 k
k 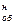 = 3
= 3 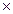 6,633 = 19,9 тыс. руб.
6,633 = 19,9 тыс. руб.
где 6,633 – коэффициент наращения для 6 платежей при i = 4 %.
На эту сумму начисляются проценты в течение следующих 2х лет.
S = 19,9 (1 + 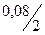 )2
)2  2 = 23,28 тыс. руб.
2 = 23,28 тыс. руб.
Альтернативное решение.
Предположим, что платежи были сделаны также и в течение последних двух лет. Тогда надо найти будущую величину аннуитета по формуле (21).
Sоб = 3  k
k 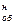 = 3
= 3  12,006 = 36,02 тыс. руб.
12,006 = 36,02 тыс. руб.
где 12,006 – коэффициент наращения для 10 платежей при i = 4 %.
Из найденной суммы надо вычесть платежи за последние два года.
S = 36,02 – (3  k
k 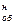 ) = 36,02 – 3
) = 36,02 – 3  4,246 = 23,28 тыс. руб.
4,246 = 23,28 тыс. руб.
где 4,246 – коэффициент наращения для 4 платежей при i = 4 %.
Альтернативное решение можно проиллюстрировать временной диаграммой:

Рис. 14. Временная диаграмма примера 23
В расчетах коэффициенты наращения аннуитета взяты из табл. 3 прил. 2.
Для определения современного (или текущего) значения аннуитета необходимо просуммировать текущие величины каждого платежа.
Пример 24.
Найти современную величину аннуитета для четырех платежей по 5 тыс. руб., которые вносились на счет в конце каждого года под 12 %.
Решение.
Для текущего аннуитета точкой локализации является начало аннуитета. Все платежи надо привести к этой точке, полученные значения сложить.
По формуле (15) найдем современное значение каждого платежа:
для первого платежа Р1 = 5 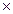
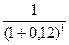 = 4,465 тыс. руб.;
= 4,465 тыс. руб.;
для второго платежа Р2 = 5 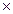
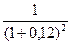 = 3,985 тыс. руб.;
= 3,985 тыс. руб.;
для третьего платежа Р3 = 5 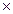
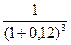 = 3,56 тыс. руб.;
= 3,56 тыс. руб.;
для четвертого платежа Р4 = 5 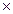
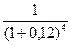 = 3,18 тыс. руб.;
= 3,18 тыс. руб.;
Сумма всех дисконтированных платежей составит:
4,465 + 3,985 + 3,56 + 3,18 = 15,19 тыс. руб.
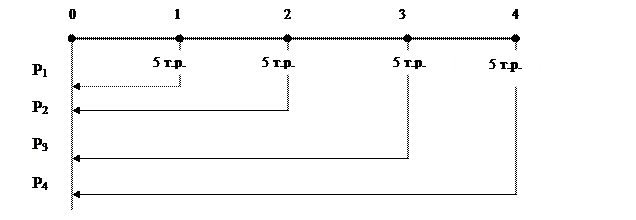
Рис. 15. Временная диаграмма примера 24
Если число платежей невелико, расчет можно вести так, как было сделано в примере. Но в любом случае проще воспользоваться формулой:
Аоб. = R 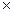
 = R
= R 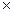 k
k 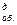 (23)
(23)
где Аоб . – современная величина обыкновенного аннуитета;
i – годовая процентная ставка;
n – число платежей;
R – периодический платеж.
Выражение в квадратных скобках является коэффициентом дисконтирования аннуитета (k 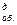 ). Его можно определить по табл. 4 прил. 2.
). Его можно определить по табл. 4 прил. 2.
Воспользуемся формулой (23) и табл. 4 прил. 2 для решения выше приведенного примера:
Аоб. = 5 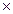 3,037 = 15,19 тыс. руб.
3,037 = 15,19 тыс. руб.
Результат получим такой же, но решение намного проще.
Зная современное значение аннуитета, можно определить величину периодического платежа:
R = A 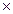
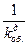 (24)
(24)
Пример 25.
Заемщик берет ссуду в 100 млн руб. под 10 % и должен погасить ее равными платежами в конце первого, второго и третьего года. Какими должны быть ежегодные платежи?
Решение.
Поскольку имеют место платежи, речь идет об аннуитетах. Известна современная величина аннуитета, т.к. ссуду заемщик берет сейчас, в настоящее время.
Для решения воспользуемся формулой (24) и табл. 4 прил. 2:
R = 100 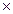
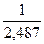 = 40, 21 млн руб.
= 40, 21 млн руб.
Пример 26.
Заемщик берет ссуду на 3 года из расчета 10 % годовых. Она должна быть погашена тремя платежами по 1 млн руб. в конце первого, второго и третьего года. Какую сумму рассчитывает получить заемщик?
Решение.
Аоб. = 1 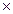 2,487 = 2,487 тыс. руб.
2,487 = 2,487 тыс. руб.
Пользуясь таблицами, рассчитать параметры аннуитета несложно, но надо быть внимательным, чтобы не перепутать современную и будущую величину аннуитета.
Как было сказано выше, аннуитет может быть не только обыкновенным, но и срочным.
Срочный аннуитет отличается осуществлением платежей не в конце, а в начале каждого интервала начисления. Это значит, что первый платеж проводится сразу же, а не через год. В отличие от обыкновенного аннуитета, на последний платеж срочного аннуитета проценты начисляются.
Примерами срочного аннуитета являются страховые взносы, арендная плата.
Чтобы вывести формулу будущей величины срочного аннуитета, модифицируют формулу (21).Это позволяет пользоваться таблицами коэффициентов обычного аннуитета.
Сравним срочный и обыкновенный аннуитеты с помощью временной диаграммы. Заметим, что срочный аннуитет начинается сразу же с первого платежа, а заканчивается одним периодом после последнего n -го платежа.

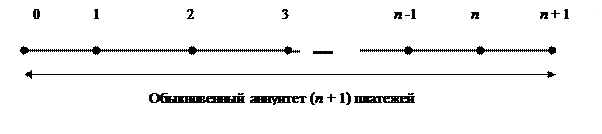
Рис. 16. Временная диаграмма обыкновенного и срочного аннуитетов
Рис. 16 показывает, что на основе расчета будущей величины обыкновенного аннуитета, состоящего из (n + 1) платежей, можно определить будущее значение срочного аннуитета, но состоящего из n платежей, поскольку последний (n + 1) платеж реально не сделан к концу последнего периода срочного аннуитета.
Таким образом, чтобы найти будущую величину срочного аннуитета, надо вычесть один платеж из будущего значения обыкновенного аннуитета, число платежей которого на 1 больше, чем у срочного аннуитета.
S 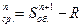 , (25)
, (25)
где S 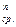 - будущая величина срочного аннуитета, состоящего из n платежей;
- будущая величина срочного аннуитета, состоящего из n платежей;
S  - будущая величина обыкновенного аннуитета, состоящего из (n +1) платежей.
- будущая величина обыкновенного аннуитета, состоящего из (n +1) платежей.
После преобразований формула (25) имеет следующий вид:
S 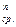 = R (k
= R (k 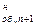 - 1 ), (26)
- 1 ), (26)
где k 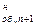 - коэффициент наращения обыкновенного аннуитета, состоящего из (n + 1) платежей.
- коэффициент наращения обыкновенного аннуитета, состоящего из (n + 1) платежей.
Формула (26) позволяет пользоваться табличными значениями коэффициентов наращения обыкновенных аннуитетов.
Пример 27.
Платежи в размере 10 тыс. руб. перечисляются на накопительный счет в начале каждого года. На них начисляются проценты по ставке 8 %. Какая сумма будет на счете к концу 5го года?
Решение.
Поскольку речь идет о срочном аннуитете, то для нахождения коэффициента наращения прибавим 1 к 5 годам. По табл. 3 прил. 2 находим коэффициент для n = 6, i = 8 %. Он равен 7,336.
S  = 10 (7,336 – 1) = 6,36 тыс. руб.
= 10 (7,336 – 1) = 6,36 тыс. руб.
Чтобы найти современное (текущее) значение срочного аннуитета, обратимся к временной диаграмме.
Заметим, что срочный аннуитет начинается сразу же с первого платежа.
На рисунке 17 видно, что современная величина срочного аннуитета, состоящего из n платежей равна сумме современной величины обыкновенного аннуитета, состоящего из (n – 1) платежей, и первого платежа.
А 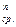 = А
= А 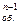 + R, (27)
+ R, (27)
где А 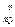 - современная величина срочного аннуитета, состоящего из n платежей;
- современная величина срочного аннуитета, состоящего из n платежей;
А 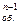 - современная величина обыкновенного аннуитета, состоящего из
- современная величина обыкновенного аннуитета, состоящего из
(n – 1) платежей.


Рис. 17. Временная диаграмма обыкновенного и срочного аннуитетов
После преобразований формула (27) имеет следующий вид: 
А 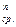 = R (k
= R (k 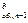 + 1 ) (28)
+ 1 ) (28)
где k 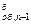 - коэффициент дисконтирования, обыкновенного аннуитета, состоящего из (n – 1) платежей.
- коэффициент дисконтирования, обыкновенного аннуитета, состоящего из (n – 1) платежей.
Значение этого коэффициента легко найти с помощью табл. 4 прил. 2.
Пример 28.
За имущество, взятое в аренду на 4 года, начислен ежегодный платеж в 60 тыс. руб., который надо вносить в начале каждого года. Арендатор хочет погасить все платежи одной суммой сразу же. Рассчитайте эту сумму, если арендодатель применил ссудную ставку 6 %.
Решение.
Необходимо определить современную величину аннуитета, исходя из следующих данных: R = 60 тыс. руб., i = 6%, n = 4. Воспользуемся формулой (28), но сначала найдем по табл. 4 прил. 2 необходимый коэффициент дисконтирования обыкновенного аннуитета, состоящего из 3х (4 – 1) платежей. Он равен 2,673. Тогда А 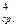 = 60 (2,673 + 1) = 220,4 тыс. руб.
= 60 (2,673 + 1) = 220,4 тыс. руб.
Следовательно, сумма в 220,4 тыс. руб., выплаченная в начале первого года, будет эквивалентна 4 платежам по 60 тыс. руб., вносимым в начале каждого года.
Некоторые инвестиции осуществляются с целью получения и использования только процентного дохода, сохраняя нетронутым первоначально вложенный капитал. К примеру, если некий филантроп изъявляет желание, чтобы музей получал годовую стипендию в размере 100 тыс. руб. пожизненно, то какую сумму ему следует пожертвовать, чтобы она приносила ежегодный доход в 100 тыс. руб.?
Если предположить, что регулярные платежи будут поступать вечно, то такой аннуитет называется бессрочным или пожизненным.
Другие примеры: дивиденды по безотзывным привилегированным акциям; облигациям, не имеющим срока погашения; всевозможные фонды, лауреаты которых получают премии и т.д.
Конечно, на практике пожизненные аннуитеты должны когда-то заканчиваться, но предположение «навсегда» все еще лежит в основе их математической трактовки. И естественно, что невозможно рассчитать будущую величину такого аннуитета. Однако расчет современного значения всех его платежей и возможен, и не сложен.
Рассмотрим случай, когда интервал начисления процентов совпадает с платежным периодом. Чтобы рассчитать первоначальный капитал, обеспечивающий пожизненную стипендию в 100 тыс. руб. в год, мы должны знать, какая ожидается процентная ставка на пожертвование. Предположим, что музей надеется на доходность в 4 %. Тогда филантроп должен был бы пожертвовать сумму в 2500 тыс. руб., поскольку именно этот капитал будет приносить годовой доход равный 100 тыс. руб. И до тех пор, пока расходуются только проценты, а вложенный капитал обеспечивает доход в 4 %, 100-тысячное вознаграждение музею может выплачиваться бесконечно долго.
Исходя из условий примера, можно записать:
А∞ 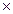 i = R или А∞ =
i = R или А∞ = 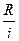 , (29)
, (29)
где А∞ - пожизненный аннуитет.
А∞ означает современную величину серии платежей, которые выплачиваются бесконечно.
Пример 29.
Выпускник университета хочет назначить годовую стипендию лучшему студенту года в размере 15 тыс. руб. Какую сумму он должен внести, если доходность инвестиций составляет 8 %, а первую стипендию предполагается выплатить через год.
Решение.
Речь идет о пожизненной ренте. Воспользуемся формулой (29):
А∞ = 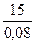 = 187,5 тыс. руб.
= 187,5 тыс. руб.
Следовательно, если выпускник университета внесет 187,5 тыс. руб., которые будут приносить доход в 8 %, то университет сможет выплачивать лучшему студенту года по 15 тыс. руб. Количество лет, в течение которых будут награждаться лучшие студенты, бесконечно.
Задания для самоподготовки
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1504; Нарушение авторских прав?; Мы поможем в написании вашей работы!