Метод обобщенных минимальных невязок

Пусть пространства K и L связаны соотношением L = A K, причем в качестве K используется подпространство Крылова K_m (n ₁, A) с выбором n ₁= r ₀/b, b=|| r ₀||₂. Для построения ортонормированного базиса воспользуемся ортогонализацией Арнольди. Вместо проектирования (2.16) рассмотрим эквивалентную задачу минимизации функционала f (x)=|| r _x||₂² на пространстве K. Так как любой вектор x из пространства (x ₀+ K _m) может быть записан в виде

x=x₀+V _m y,

где y вектор размера m. Таким образом, задачу минимизации функционала можно переписать как

y _m =argmin_y||b–A(x₀+V_my)||₂².

Вычислительная схема, построенная с использованием таких предпосылок, называется методом обобщенных минимальных невязок (GMRES).

С использованием определения вектора n ₁ и соотношений (2.30), (2.32) имеем

r=b–A(x₀+V _m y)=V _{m +1}(be₁– y).

Поскольку матрица V _{m +1} составлена из ортонормированных столбцов, справедливо равенство

y(y)=f(x0+V m y)=||be1– y||2^2.

(2.47)

Таким образом, для нахождения коэффициентов линейного комбинирования векторов { n _i } в GMRES необходимо решить СЛАУ

.

(2.48)

которая является переопределенной (так как матрица имеет размерность (m +1)´ m).

Матрица системы (2.48) имеет верхнюю хессенбергову форму. Поэтому (2.48) проще всего решать с помощью предварительного приведения к верхнетреугольному виду; последняя строка при этом обнуляется. С учетом хессенберговой формы наиболее простым вариантом оказываются вращения Гивенса. Всего необходимо m таких вращений G ₁, G ₂,…, G _m, причем G _k строится так, чтобы его применение к (h_kk, h_{k +1, k}) ^T обнуляло второй компонент этого вектора.

Структура матриц G ₁ и G ₂ имеет вид

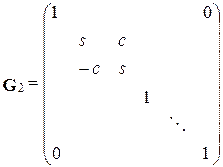
Числа s и c связаны соотношением s ²+ c ²=1 (это позволяет их интерпретировать как синус и косинус некоторого угла) и определяются как:

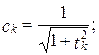
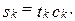
Очевидно, что при программной реализации нет необходимости в непосредственном хранении матриц вращения G _i, так как каждая такая матрица полностью определяется двумя числами – косинусом и синусом угла поворота – и индексами компонент вектора, к которым применяется вращение.

Основной проблемой в GMRES является выбор размерности m пространства K; хранение базисных векторов этого пространства определяет основные затраты памяти при программной реализации метода, составляющие mN чисел. Наиболее распространенной модификацией GMRES является перезапускаемый GMRES или GMRES(m). Выбирается некоторая размерность m < N, определяемая, по существу, лишь доступным объемом памяти, и после обновления решения x = x ₀+ V _m y _m оно принимается за новое начальное приближение, после чего процесс повторяется.

Далее приведен алгоритм предобусловленного метода GMRES(m) с вращениями Гивенса.

Алгоритм метода GMRES( m ) с вращениями Гивенса

Если необходимо построить матрицу предобусловливателя M

Выбрать m < N и произвольное начальное приближение x⁽⁰⁾

z = b – A x⁽⁰⁾

g=||z||₂

Найти r⁽⁰⁾ из системы M r⁽⁰⁾ =z

b = ||r⁽⁰⁾||₂

Создать ((m + 1) ´ m) - матрицу H

Создать вектор (m + 1) - вектор q

Для N_it =1, 2, … до сходимости или до N_it^max

H = 0; q= b e₁

n₁= r⁽⁰⁾/b

Для i =1,…, m

z=An^{( i )}

Найти w из системы Mw=z

Для k =1,…, i

h_ki =(w, n^{( k)})

w=w– h_ki n^{( k )}

увеличить k

h_{i +1, i} =||w||₂

n^{( i +1)}=w/ h_{i +1 ,i}

Для k =1,…, i –1

(h _{1 i} ,…, h_{i +1 ,i} ) ^T =G _k (h _{1 i} ,…, h_{i +1 ,i} ) ^T

увеличить k

Построить G _i так, что [G _ih _{×, i} ] _{i +1}=0

q=G _i q

увеличить i

Решить треугольную СЛАУ H_{1: p ,1: p} y=q_{1: p}

z=b–Ax⁽⁰⁾

Найти r₀ из системы Mr₀=z

b=||r⁽⁰⁾||₂

Продолжать пока b/g³ tol

Алгоритм начинается с того, что требуется задать произвольное начальное условие x^{( 0)} (третий параметр метода). Итерационный процесс продолжается до тех пор, пока не будет получено решение, с точностью определяемое параметром tol (четвертый параметр)или при достижении максимального числа итераций N_it^max (пятый параметр). Также необходимо, чтобы пользователь определил размерности m (шестой параметр).В случае необходимости использовать метод без предобусловливани необходимо инициализировать седьмой параметр нулем. В противном случае необходимо задать:

- 10 в случае использования метода с предобусловливанием, основанном на LU-разложении с выбором структуры разреженности, основанном на норме строки;

- 11 в случае использования метода с предобусловливанием, основанном на LU-разложении с выбором структуры разреженности, основанном на норме столбца;

- 12 в случае использования метода с предобусловливанием, основанном на LU-разложении с выбором структуры разреженности, основанном на норме матрицы;

-20 в случае использования метода с предобусловливанием, основанном на ILU(0) разложении с выбором структуры разреженности, основанном на норме строки;

- 21 в случае использования метода с предобусловливанием, основанном на ILU(0) разложении с выбором структуры разреженности, основанном на норме столбца;

-22 в случае использования метода с предобусловливанием, основанном на ILU(0) разложении с выбором структуры разреженности, основанном на норме матрицы.

Также для использования метода с предобусловливанием необходимо задать точность обнуления (t) определяемую восьмым параметром.

Пример использования метода GMRES(m) с вращениями Гивенса в системе TALGAT:

- действительный случай: SET "solve" GMRES_r real_m right_r 0. 1.e-8 150 15 10 1.e-4;

- комплексный случай: SET "solve" GMRES complex_m right_c 0. 1.e-8 150 15 10 1.e-4.

Дата добавления: 2014-12-27