
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предобусловливание
|
|
|
|
Вычисление итерационными методами зависит от обусловленности матрицы А,оцениваемой числом обусловленности cond A =|| A ||×|| A –1||»|l max |/|l min |. С ростом cond A обусловленность ухудшается, и для ряда проблем сходимость может оказаться очень медленной и поэтому итерационный процесс может застопорится или даже оборваться. Однако применение так называемого предобусловливания улучшает сходимость к требуемому решению.
Пусть М – некоторая невырожденная матрица размерности N. Домножив (1.1) на матрицу M –1, получим систему
| M–1Ax=M–1b, | (2.40) |
которая в силу невырожденности M имеет то же точное решение x *. Введя обозначения 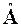 = M –1 A и
= M –1 A и 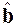 = M –1 b, (2.40) примет вид
= M –1 b, (2.40) примет вид
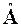 x= x= 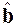 . .
| (2.41) |
Хотя (2.41) алгебраически эквивалентна (1.1), спектральные характеристики матрицы 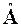 отличаются от характеристик матрицы A, что, вообще говоря, ведет к изменению скорости сходимости численных методов для (2.41) по отношению к (1.1) в конечной арифметике.
отличаются от характеристик матрицы A, что, вообще говоря, ведет к изменению скорости сходимости численных методов для (2.41) по отношению к (1.1) в конечной арифметике.
Процесс перехода от (2.1) к (2.41) с целью улучшения характеристик матрицы для ускорения сходимости к решению называется предобусловливанием, а матрица M –1– матрицей предобусловливателя. Из (2.40) сразу же вытекает важное требование: матрица M должна быть близка к матрице A. Выбор M = A сразу же приводит (1.1) к виду Ix = A –1 b, однако не имеет практического смысла, так как требует нахождения A –1, что по существу и сводится к решению (1.1). Вторым естественным требованием является требование легкой вычислимости матрицы M.
Невязкой системы (1.1), соответствующей вектору x, называется вектор r = b – Ax = A (x *– x), где x *– точное решение. Невязка 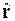 системы (2.41) связана с невязкой системы (1.1) очевидным соотношением
системы (2.41) связана с невязкой системы (1.1) очевидным соотношением
M 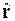 =r, =r,
| (2.42) |
которое справедливо и для матрично-векторных произведений z = Aq и  =
= 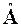 q:
q:
 = = 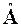 q=M–1AqÞ M q=M–1AqÞ M  =Aq=z. =Aq=z.
| (2.43) |
Это позволяет вместо явного перехода от (1.1) к (2.41) вводить в схемы методов корректирующие шаги для учета влияния предобусловливающей матрицы. Данный подход называется неявное предобусловливание. Явное предобусловливание требует нахождениия матрицы М –1 и умножения матрицы предобусловливания на вектор в каждой. В данной версии системы TALGAT реализовано использование только неявного предобусловливания.
Из (2.43) следует еще одно условие: структура матрицы предобусловливателя должна допускать легкое и быстрое решение «обратных к предобусловливателю» систем вида M  = z.
= z.
Таким образом:
Ø M должна быть по возможности близка к матрице A;
Ø M должна быть легко вычислима;
Ø M должна быть легко обратима.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 696; Нарушение авторских прав?; Мы поможем в написании вашей работы!