
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Биортогонализация Ланцоша
|
|
|
|
Алгоритм ортогонализации Арнольди, рассмотренный ранее, для построения каждого нового вектора n k требует нахождения (k –1) скалярных произведений и столько же операций линейного комбинирования. Однако, как оказывается, при отказе от требования ортогональности базиса в пользу некоторого более общего условия можно построить процедуру меньшей сложности.
Системы векторов 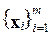 и
и 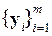
 называются биортогональными, если скалярное произведение (x i, y i) обращается в ноль при i ¹ j. В случае x i º y i условие биортогональности сводится к обычному условию ортогональности. Пусть векторы n 1 и w 1 таковы, что (n 1, w 1)¹0 и пусть системы векторов
называются биортогональными, если скалярное произведение (x i, y i) обращается в ноль при i ¹ j. В случае x i º y i условие биортогональности сводится к обычному условию ортогональности. Пусть векторы n 1 и w 1 таковы, что (n 1, w 1)¹0 и пусть системы векторов 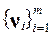 и
и 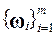 определяются соотношениями:
определяются соотношениями:
| n i +1=An i –a i n i –b i n i –1, n0º0; | (2.33) |
| w i +1=A T w i –a i w i –b i w i –1, w0º0; | (2.34) |
| a i =(An i, w i)/)(n i,w i); | (2.35) |
| b i =(n i, w i)/(n i –1, w i –1), b1º0. | (2.36) |
Тогда
Ø системы 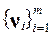 и
и 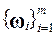 являются биортогональными;
являются биортогональными;
Ø каждая система 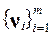 и
и 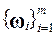 является линейно независимой и образует базис в Km (n 1, A) и Km (w 1, A T) соответственно.
является линейно независимой и образует базис в Km (n 1, A) и Km (w 1, A T) соответственно.
Процедура построения векторов n и w согласно формулам (2.33)–(2.36) называется биортогонализацией Ланцоша.
Очевидно, что (2.33) является частным случаем (2.29), где из всей суммы оставлены только два последних слагаемых; точно так же (2.34) является частным случаем (2.29), записанной для матрицы A T и вектора w 1. При этом коэффициенты ортогонализации в (2.33) и (2.34) одинаковы. Из сказанного следует, что можно записать аналог матричной формулы (2.31)
| W mT AV m =T m, | (2.37) |
где T m – симметричная трехдиагональная матрица, элементы которой определяются соотношениями
| [T m ] ii =a i (n i, w i); | (2.38) |
| [T m ] i +1, i =[T m ] i , i +1=b i (n i, w i), | (2.39) |
выводимыми из (2.39) – (2.40).
Основным недостатком биортогонализация Ланцоша является возможность возникновения ситуации, когда (n i, w i)=0; при этом продолжение процесса становится невозможным из-за неопределенности коэффициента b i +1.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 722; Нарушение авторских прав?; Мы поможем в написании вашей работы!