
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неполное LU-разложение
|
|
|
|
Предобусловливание основанное на классических методах
Ранее было показано, что методы Якоби и Гаусса-Зейделя, а также SOR и SSOR могут быть представлены в виде (2.8). Другой формой этого выражения является
| x k +1=Gx k +f, | (2.44) |
которое получается из (2.14) домножением левой и правой частей на K –1. Проведя аналогию с (2.1) и (2.2), нетрудно увидеть, что (2.44) можно рассматривать как итерационную схему, построенную для решения СЛАУ
| (I–G)x=f, | (2.45) |
в которой
| f=K–1b; G=K–1R=K–1(K–A)=I–K–1A. |
Таким образом, система (2.51) эквивалентна системе
| K–1Ax=K–1b, |
т.е. предобусловленной СЛАУ (2.1) с матрицей предобусловливания K. Для методов Якоби, Гаусса-Зейделя, SOR и SSOR эти матрицы соответственно, равны (K заменено на M):
| MJ=D; |
| MGS=D–E; |
MSOR 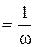 (D–wE); (D–wE);
|
MSSOR 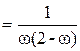 (D–wE)D–1(D–wF). (D–wE)D–1(D–wF).
|
Скалярные множители 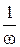 и
и 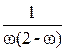 при практических реализациях SOR и SSOR-предобусловливания обычно не учитываются, так как дают лишь масштабирование, практически не влияющие на скорость сходимости.
при практических реализациях SOR и SSOR-предобусловливания обычно не учитываются, так как дают лишь масштабирование, практически не влияющие на скорость сходимости.
При w=1 получается симметричный метод Гаусса-Зейделя (SGS)
| MSGS=(D–E)D–1(D–F). |
Заметив, что (D – E) соответствует нижнетреугольной части матрицы A, а (D – F) верхнетреугольной части, то
| MSGS=LU, |
где
| L=(D–E)D–1=I–ED–1, U=D–F. |
Таким образом для решения систем вида w = M SGS–1 x необходимо последовательно решить
| (I–ED–1)z=x, (D–F)w=z. |
Исторически предобусловливание, как собственно и итерационные методы вообще, использовалось для решения разреженных СЛАУ большой размерности. Поэтому использование предобусловливания для решения СЛАУ с плотными матрицами необходимо использовать с некоторыми добавлениями о которых речь пойдет позже.
Для систем с разреженными матрицами хорошим предобусловливанием является неполное LU-разложение. Данное разложение заключается в представлении матрицы в виде
| M=LU+R, | (2.46) |
где L и U как и прежде нижне- и верхнетреугольные матрицы, соответственно, а матрица R является матрицей ошибки. Тогда приближенное представление M» LU называется неполным LU-разложением матрицы M или коротко её ILU-разложением. Как хорошо известно, в результате реализации стандартного LU-разложения на месте исходной матрицы находится результат разложения, т.е. матрицы L и U, одна из которых имеет единичную диагональ.
Наиболее простым вариантом является ILU(0) разложение. Оно заключается в применении LU-разложения к матрице M, но если mij = 0, то полагается lij = 0 или uij = 0. Поскольку в рассматриваемой задаче матрица M плотная, то применение ILU(0) не целесообразно, без предварительного процесса разрежевания.
С учетом вышесказанного представление матрицы предобусловливания в виде удобном для использования итерационного метода с неявным преобусловливанием (M» LU) требует осуществления двух этапов. На первом этапе определяется структура разреженности матрицы М (путем предфильтрации матрицы А), т.е. mij = aij, если пара индексов (i, j) соответствует предписанной структуре и mij = 0 в противном случае (данный этап более подробно рассмотрен ниже). На втором этапе производится собственно само ILU-разложение, в частности ILU(0).
Алгоритм ILU(0) разложения
| Для i =1,… N |
| w= ai * |
| Для k =1,… i –1и wk ¹0 |
| wk = wk / ukk |
| Для j = k +1,… N |
| w=w– wk × uk * |
| Увеличить j |
| Увеличить k |
| lij = wj, для j =1,… i -1 |
| uij = wj, для j = i,… N |
| Увеличить i |
Очевидно, что построенная таким образом матрица LU удовлетворяет всем требованиям к матрице предобусловливателя. Действительно, она близка к матрице A; она легко вычислима по приведенному выше не сложному алгоритму; наконец, она легко обратима, так как является произведением двух треугольных матриц. Таким образом, выбор M = LU является достаточно хорошим способом предобусловливания.
В данной версии системы реализовано нахождение матрицы предобусловливания как с помощью ILU(0), так и с помощью стандартного LU-разложения.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 3290; Нарушение авторских прав?; Мы поможем в написании вашей работы!