Вычисление функционала качества на траекториях движения объекта

Как отмечено в разделе 1, для задачи параметрической оптимизации необходимо сформировать целевую функцию (функционал), количественно характеризующую поведение системы (объекта), зависящую от варьируемых (изменяемых) параметров этого объекта. В качестве примера целевая функция может определена как площадь, образуемая отклонением реальной траектории движения относительно заданной.

Математически данный функционал записывается как интеграл:

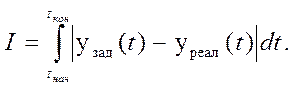
Понятно, что это не единственный способ задания целевой функции. Под знаком интеграла может быть не обязательно абсолютная величина разности, а ее квадрат, не только отклонение реальной траектории движения от заданной, но и производная этого отклонения:

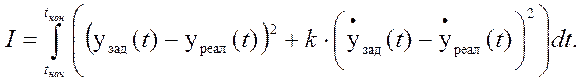
Следует отметить, что целевая функция, как и значение весового коэффициента k, задается экспертом, специалистом в данной предметной области. Программист-математик всего лишь реализует вычисление этого функционала. С учетом того, что объект представлен математической моделью в виде системы дифференциальных уравнеий (как показано в предыдущем разделе), поведение этого объекта может быть получено численными методами. Решение системы дифференциальных уравнений на ЭВМ всегда выполняется пошагово, путем получения последовательных значений как вектора состояния системы 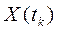, так и выходной координаты , 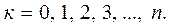В этом случае вычисление функционала I может быть сведено к суммированию:

Здесь , - шаг интегрирования, .

Таким образом, задача вычисления функционала есть последовательное суммирование, выполняемое на каждом шаге решения системы дифференицальных уравнений, в соответствии с алгоритмом, в вычислительном блоке 4: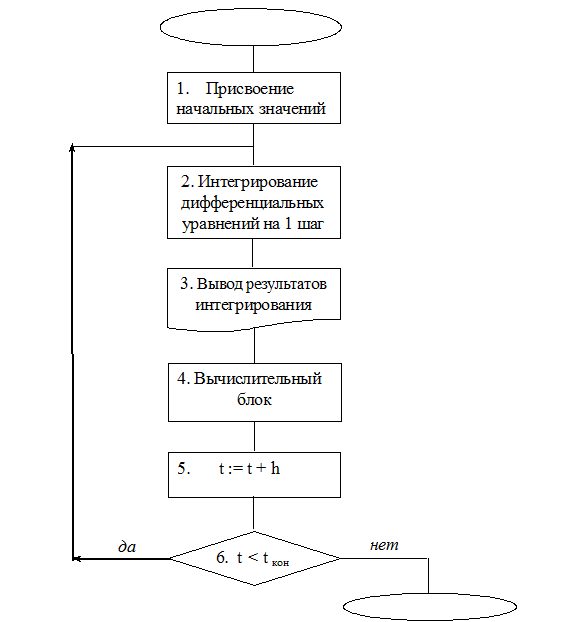

Рис. Схема алгоритма программы интегрирования системы дифференциальных уравнений и вычисления функционала.

Полученную программу следует преобразовать в подпрограмму-функцию, возвращающую значение функционала, входными параметрами которой должны быть изменяемые (варьируемые) параметры объекта. Блок 3 алгоритма (вывод результатов интегрирования) можно исключить.

Следует отметить, что целевая функция (функционал), используемая в задаче параметрической оптимизации, определяется не обязательно интегральной оценкой качества, как указано в начале данного раздела. В некоторых случаях целевая функция может быть сформулирована по переходной характеристике системы относительно задающего воздействия.

Количественная оценка качества системы по переходной характеристике определяется показателями: перерегулированием σ, временем первого согласования τ, временем достижения первого амплитудного значения, временем регулирования (временем переходного процесса) t_п.

Перерегулирование (определяется величиной первого выброса) - отношение разности максимального значения переходной характеристики и ее установившегося значения к величине установившегося значения. Измеряется обычно в процентах.

.

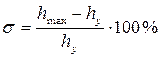Время регулирования - длительность переходного процесса. Правда, в идеальной системе переходный процесс бесконечен. Поэтому временем регулирования считают тот интервал времени, по истечении которого отклонения переходной характеристики от установившегося значения не превышают D. Значения D обычно принимают 5%, 2%, а иногда и 1%. Но такой выбор всегда оговаривается.

В этом случае целевая фукнкция может быть задана как:

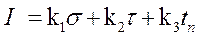, где - весовые коэффициенты, задаваемые экспертами.

Имеется ввиду, что чем лучше переходная характеристика (чем меньше перечисленные выше показатели), тем лучше система будет отрабатывать произвольное задающее воздействие.

Дата добавления: 2014-12-27