
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы минимизации функций нескольких переменных
|
|
|
|
Определения, сформулированные выше для функции одной переменной, можно обощить для случая функций многих переменных. Пусть функция п переменных J (Х) определена на множестве  .
.
1. Точка х*Î Un, называется точкой глобального минимума функции J (Х), если для всех х*Î Un выполняется неравенство J (x*) £ J (Х). Значение 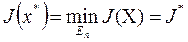 называется минимумом функции. Множество всех точек глобального минимума функции J (Х) обозначают через U *.
называется минимумом функции. Множество всех точек глобального минимума функции J (Х) обозначают через U *.
Замечание. Если U * ¹ 0, то вместо минимума функции J (Х) иногда рассматривают ее точную нижнюю грань  , определение которой в n –мерном случае практически не отличается от определения для одномерной функции.
, определение которой в n –мерном случае практически не отличается от определения для одномерной функции.
2. Точка 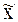 называется точкой локального минимума функции J (Х), если существует e–окрестность точки
называется точкой локального минимума функции J (Х), если существует e–окрестность точки 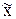 : U n (
: U n (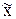 )={Х | r(Х,
)={Х | r(Х, 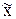 ) < e} такая, что для всех х*Î U n (
) < e} такая, что для всех х*Î U n (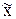 ) выполняется неравенство J (
) выполняется неравенство J (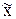 ) £ J (Х).
) £ J (Х).
3. Если допустимое множество Un в задаче минимизации (максимизации) функции n переменных совпадает со всем пространством E n, то говорят о задаче безусловной оптимизации
 , x Î E n.
, x Î E n.
В задачах минимизации особую роль играют выпуклые функции, так как локальный минимум выпуклой функции является глобальным минимумом, а строгая выпуклость обеспечивает еще единственность глобального минимума.
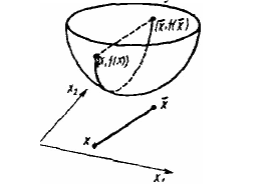
В общем случае рассматривается задача 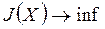 ,
,
предполагая, что функция  непрерывно дифференцируема на
непрерывно дифференцируема на  . Согласно определению дифференцируемости функции
. Согласно определению дифференцируемости функции
 ,
,
где  . Если
. Если  , то при достаточно малых
, то при достаточно малых  приращение
приращение 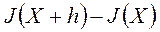 будет определяться дифференциалом функции
будет определяться дифференциалом функции 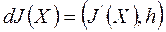 .
.
Справедливо неравенство Коши-Буняковского
 ,
,
причем если  , то правое неравенство превращается в равенство только при
, то правое неравенство превращается в равенство только при  , а левое неравенство – при
, а левое неравенство – при  , где
, где  . Отсюда ясно, что при
. Отсюда ясно, что при  направление наискорейшего возрастания функции
направление наискорейшего возрастания функции  в точке Х совпадает с направлением градиента
в точке Х совпадает с направлением градиента  , а направление наискорейшего убывания – с направлением антиградиента
, а направление наискорейшего убывания – с направлением антиградиента  .
.
Это замечательное свойство градиента лежит в основе ряда итерационных методов минимизации функций нескольких переменных.
Большинство методов, применяемых для решения задачи минимизации функций нескольких переменных, являются итерационными методами спуска, для которых каждая итерация (шаг) приводит к уменьшению значения целевой функции:
 .
.
В численных методах индекс итерации размещается (чаще всего) сверху справа от обозначения итеративной точки, если она – векторная величина. Это позволяет сохранить обозначения компонент вектора с помощью нижнего индекса.
Все методы спуска работают по единой схеме:
1. Выбирается начальное приближение – некоторая точка  и каким-то образом выясняется, что
и каким-то образом выясняется, что  не есть точка минимума
не есть точка минимума  . Целесообразно использовать всю имеющуюся информацию о поведении целевой функции
. Целесообразно использовать всю имеющуюся информацию о поведении целевой функции  , чтобы выбрать
, чтобы выбрать  поближе к точке минимума
поближе к точке минимума  .
.
2. Пусть приближение 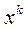 к точке минимума
к точке минимума  найдено. Выбирается вектор
найдено. Выбирается вектор  , такой, что для всех достаточно малых
, такой, что для всех достаточно малых  справедливо неравенство
справедливо неравенство  .
.
Вектор  , а иногда и сам вектор
, а иногда и сам вектор  называется направлением спуска.
называется направлением спуска.
3. Определяется величина шага спуска по направлению  , то есть положительное число
, то есть положительное число  , для которого выполняется неравенство
, для которого выполняется неравенство
 .
.
4. За очередное приближение к точке минимума принимается
 .
.
5. Проверяется выполнение критерия окончания итераций (об этом смотри ниже). Если критерий выполняется, то итерации прекращают и полагают  . В противном случае возвращаются к п. 2.
. В противном случае возвращаются к п. 2.
Последовательность точек  генерируемая методом спуска, называется траекторией спуска.
генерируемая методом спуска, называется траекторией спуска.
Критерием прекращения процесса вычислений на k -м шаге часто выбирается близость градиента к нулю: 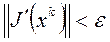 .
.
При необходимости проводится дополнительное исследование поведений функции в окрестности точки 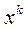 для выяснения того, достигается ли в точке
для выяснения того, достигается ли в точке 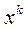 минимум функции
минимум функции  или не достигается. В частности, если
или не достигается. В частности, если  – выпуклая функция, то в стационарной точке всегда достигается минимум.
– выпуклая функция, то в стационарной точке всегда достигается минимум.
Помимо сравнения градиента с нулем используются также критерии: 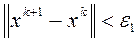 и
и 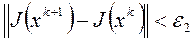 , где
, где  - заданные положительные числа. Нередко используют различные сочетания этих трех критериев.
- заданные положительные числа. Нередко используют различные сочетания этих трех критериев.
Все методы спуска решения задачи безусловной минимизации различаются либо выбором направления спуска, либо способом движения вдоль направления спуска. В любом случае на каждом шаге метода после определения направления спуска  задача минимизации сводится к вычислению шага
задача минимизации сводится к вычислению шага  в этом направлении, при котором
в этом направлении, при котором  . Иными словами, на каждом шаге минимзации функции нескольких переменных необходимо решать задачу минимизации функции одной переменной:
. Иными словами, на каждом шаге минимзации функции нескольких переменных необходимо решать задачу минимизации функции одной переменной:
 .
.
Проблемы решения данной задачи были рассмотрены в предыдущем пункте. Следовательно, для нахождения 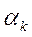 необходимо написать функцию
необходимо написать функцию  , где с учетом
, где с учетом 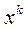 и
и 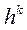 вычислялись бы последовательно
вычислялись бы последовательно  и
и  . Значения
. Значения 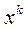 и
и 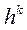 удобно передавать в функцию
удобно передавать в функцию  через общую область (если используется язык ФОРТРАН), или сделать их глобальными переменными (в случае применения языков программирования ПАСКАЛЬ либо Си). Далее, воспользовавшись уже готовой функцией поиска минимума функции от одной переменной, определяется искомое
через общую область (если используется язык ФОРТРАН), или сделать их глобальными переменными (в случае применения языков программирования ПАСКАЛЬ либо Си). Далее, воспользовавшись уже готовой функцией поиска минимума функции от одной переменной, определяется искомое 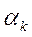 =
= 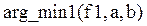 .
.
На этом этапе вычислительного процесса необходимо предварительно задаться отрезком 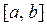 . В случае задачи безусловного поиска глобального минимума унимодальной функции величина его может быть произвольной. Но если область определения J (Х) ограничена, либо решается задача отыскания локального минимума J (Х), следует ввести ограничения и на величину шага
. В случае задачи безусловного поиска глобального минимума унимодальной функции величина его может быть произвольной. Но если область определения J (Х) ограничена, либо решается задача отыскания локального минимума J (Х), следует ввести ограничения и на величину шага 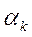 в направлении
в направлении 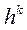 . Рекомендуется выбирать значения границ отрезка
. Рекомендуется выбирать значения границ отрезка 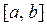 , которому должен принадлежать искомый
, которому должен принадлежать искомый 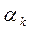 , с учетом выполнения следующего условия:
, с учетом выполнения следующего условия:
Любая компонента вектора  должна отличаться от соответствующей компоненты вектора
должна отличаться от соответствующей компоненты вектора 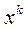 не более чем в 2-3 раза.
не более чем в 2-3 раза.
Таким образом, перед обращением к функции 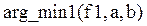 необходимо для определения a и b решить соответствующую систему неравенств.
необходимо для определения a и b решить соответствующую систему неравенств.
Имеет смысл организовать проверку начальных шагов процесса поиска минимума по нескольким переменным. Для этой цели следует выполнить сечение J (Х) из точки 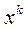 в направлении
в направлении 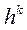 , задавая различные значения
, задавая различные значения  и вычисляя
и вычисляя 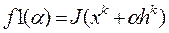 . По полученному множеству значений построить соответствующую кривую и сравнить ее минимум с результом функции
. По полученному множеству значений построить соответствующую кривую и сравнить ее минимум с результом функции 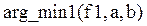 .
.
В том случае, когда область определения Un функции J (Х) ограничена 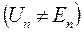 , в функцию
, в функцию  необходимо ввести соответствующие корректирующие операторы:
необходимо ввести соответствующие корректирующие операторы:
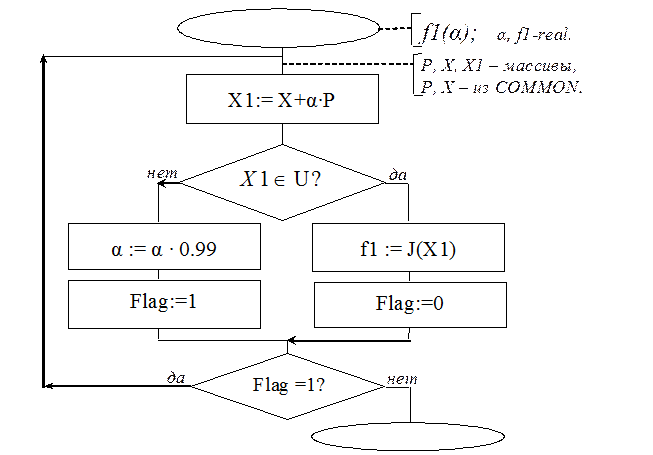 Измененное в
Измененное в 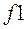 значение
значение  возвратится (через параметр) в вызывающую подпрограмму (функцию).
возвратится (через параметр) в вызывающую подпрограмму (функцию).
В предложенном алгоритме коэффициент 0,99 может быть изменен с учетом требуемой точности отыскания минимума функции (чем точнее нужен результат, тем больше девяток будет в нем после запятой).
Полученную программу (как и для скалярного случая) следует протестировать на различных эталонных функциях от нескольких переменных. Имеет смысл проверить в тестовых примерах и ограниченность области определения J (Х), например, положительность (отрицательность) некоторых переменных.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 2144; Нарушение авторских прав?; Мы поможем в написании вашей работы!