Минимизация целевой функций задачи параметрической оптимизации

После успешного тестирования программы минимизации фунции нескольких переменных можно приступить непосредственно к задаче параметрической оптимизации исходной системы. Для этого необходимо по реализованным в пунктах 5.1 и 5.2 алгоритмам выполнить минимизацию целевой функции, полученной в разделе 4.

Данная задача практически ничем не отличается от минимизации эталонных функций нескольких переменных. Следует только внимательно отнестись к использованию глабальных переменных (описанию общих областей COMMON), описанию (декларации) всех переменных и их инициализации.

В буферной функции необходимо обеспечить неотрицательность варьируемых переменных системы (ограничить их положительной величиной, близкой к 0, например 0.000001) и без ошибок обратиться к минимизируемой целевой функции J (Х) (проконтролировать список параметров в описании J (Х) и вызове ее).

Как было отмечено в разделе 5.2, имеет смысл проверить начальные шаги процесса поиска минимума целевой функции, выполнив сечение J (Х) из точки 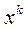в направлении 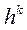, задавая различные значения и вычисляя 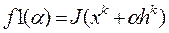(до обращения к функции 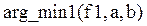). Затем сравнить минимум полученной кривой с результатом выполнения .

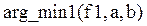Рекомендуется на каждом шаге задачи параметрической оптимизации выводить на экран и записывать в файл значения: 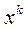, направление 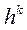, полученное 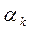и значение J (Х) в очередной точке . Данная информация позволит проанализировать ход вычислительного процесса и проверить соответствие его результатов реализованным в программе методам поиска минимума. Кроме того, по полученным значениям можно построить траекторию движения к минимуму функционала в плоскостях варьируемых параметров с целью визуализации работы программы.

По окончании работы программы имеет смысл получить кривые переходного процесса исходной системы (см. разделы 3 и 4) с начальными и оптимальными значениями ее параметров. Анализ этих кривых позволит дать визуальное представление об улучшении качества системы после оптимизации.

Заключение

Параметрическая оптимизация динамического объекта – процесс состоящий из множества этапов, на каждом из которых приходится решать определённые задачи.

С помощью системы дифференциальных уравнений описывается поведение системы во времени.

В результате решения системы дифференциальных уравнений можно получить количественную характеристику (функционал) поведения (качества) динамической системы.

Используя методы минимизации функций нескольких переменных, в совокупности с методами минимизаций функций одной переменной, можно решить задачу по уменьшению значения функционала системы.

Список используемой литературы

1. Васильев Ф.П. Численные методы решения экстремальных задач: Учебное пособие для вузов. – 2-е издание, переработанное и дополненное – М.: Наука. Главная редакция физико-математической литературы, 1988. – 552 с.

2. Васильев Ф. П. Методы оптимизации. – М.: Факториал Пресс, 2002. – 824 с.

3. Черноруцкий И.Г. Методы оптимизации в теории управления: Учебное пособие: доп. Мин. обр. РФ/ И. Г. Черноруцкий. – СПб.: Питер, 2004. – 256 с.

4. Корнеенко В. П. Методы оптимизации: Учебник / В. П. Корнеенко. – М.: Высш. шк., 2007. – 664 с.

5. Пантелеев А.В. Методы оптимизации в примерах и задачах: Учебное пособие: рек. УМО/ А. В. Пантелеев, Т. А. Летова. – 3-е изд., стер.. – М.: Высш. шк., 2008. – 544 с.

6. Измаилов А.Ф. Численные методы оптимизации: Учебное пособие: рек. УМС/ А. Ф. Измаилов, М. В. Солодов. – 2-е издание, переработанное и дополненное - М.: Физматлит, 2008. – 320 с.

7. Тарасик В.П. Математическое моделирование технических систем. Учебник для вузов. – Мн.: Дизайн-ПРО, 2004. – 640 с.

8. Аверченков В. И. Основы математического моделирования технических систем: Учебное пособие / В. И. Аверченков, В. П. Федоров, М. Л. Хейфец. – 2-е издание, стереотипное – М.: Флинта, 2011. – 271 с.

Дата добавления: 2014-12-27