О минимизации функций одной переменной

Минимизация целевой функции

Автоматизированные методы параметрической оптимизации (минимизации целевой функции) основаны на численных методах поиска минимума функций одной и нескольких переменных. И, как показывает практика, большинство методов минимизации функции нескольких переменных используют методы минимизации функции одной переменных.

Задачи одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси:

Максимизация целевой функции 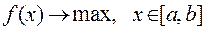эквивалентна минимизации противоположной функции: поэтому, не умаляя общности, можно рассматривать только задачи поиска минимума.

Имеют место следующие определения:

1. Число х* Î U = [a, b] называется точкой глобального (абсолютного) минимума или просто точкой минимума функции f (x) на множестве U, если f (x *) £ f (x) для всех хÎ U.

Значение f * = f (x *) = 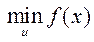называют глобальным (абсолютным) минимумом или просто минимумом функции f (x) на множе­стве U.

2. Число Î U = [a, b] называется точкой локального минимума функции f (x), если для всех x Î U, достаточно близких к 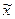, то есть, если существует e > 0 такое, что это неравенство выполняется для лю­бого .

3. Пусть функция f (x) ограничена снизу на множестве U = [a, b], то есть f (x) ³ А > – ∞ для всех х Î U. Число f _* называется точной нижней гранью функции f (x)на множестве U (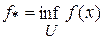), если f (x) f _* при всех х Î U и для любого e > 0 найдется точка x _e Î U такая, что f (x _e) < f _* + e (то есть сре­ди значений f (x) на множестве U найдутся как угодно близкие к f _*).

Для неограниченных снизу функций f (x) полагают f _* = – ∞.

4. Из математического анализа известно (со­гласно теореме Вейерштрасса), чтонепрерывная на замкнутом ограниченном множестве функция достигает на этом множестве своих минимального и макси­мального значений.

5. Функция f (x) называется унимодальной на от­резке [ а; b ], если она непрерывна на [ а; b ] и существуют числа a и b, 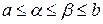, такие, что:

1) если а < a, то на отрезке [ a; a] функция f (x) монотонно убывает;

2) если b < b, то на отрезке [b; b ] функция f (x) монотонно возра­стает;

3) при х Î [a; b] f (x) = f ^* = .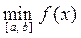

Унимодальные функции об­ладают свойством: их локаль­ный минимум является одновременно и глобальным.

Применение некоторых методов одномерной минимизации воз­можно только в случае, если скорость изменения целевой функции f (х) на любом участке отрезка [ а; b ] ограничена некоторым числом, од­ним и тем же для всех участков. То есть f (х) удов­летворяет на [ а; b ] условию Липшица.

6. Функция f (х) удовлетворяет на отрезке [ а; b ] ус­ловию Липшица, если существует такое число L > 0 (константа Липшица), что для всех х' и х", принадлежащих [ а; b ], выполняется неравенство .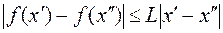

Для практического определения константы Липшица используется формула конечных приращений: для произвольных точек х', х" Î[ а; b ] имеем: , где x– некоторая точка, лежащая между х' и х". Отсюда с учетом условия 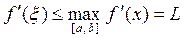определяется искомая величина.

Для решения задачи минимизации функции f (х) на отрезке [ а; b ] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью в результате определения конечного числа значений функции f (х) и ее производных в некоторых точках отрезка [ а; b ]. Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации.

Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений f (х) в заданных точках.

Самым слабым требованием на функ­цию f (х), позволяющим использовать прямые методы, является ее унимодальность. Поэтому для упрощения задачи будем считать функцию f (х) унимодальной на отрезке [ а; b ](что справедливо в окрестности локального минимума).

К прямым методам поиска минимума функции f (х) на отрезке [ а; b ] относятся метод перебора, методы исключения отрезка (деления отрезка пополам и золотого сечения), методы парабол, касательных, ломаных и так далее. В методах парабол, касательных, ломаных рекомендуется на каждом их шаге использовать метод исключения отрезков. Данный прием позволит организовать определение минимума функции f (х) с заданной точностью.

Наименее эффективным из перечисленных является метод перебора. Для обеспечения заданной точности ε нахождения минимума необходимо выполнить деление отрезка на n частей: . В остальных методах точность будет достигнута, когда длина последнего вложенного отрезка будет сопоставима с величиной заданного ε.

Для большинства практических задач является достаточным, когда величина заданной погрешности определяется в пределах одного процента от длины исходного отрезка [ а; b ], то есть принимают .

В тех случаях, когда минимум функции f (х) будет на границе множества U = [a, b], то есть в точках a или b, можно попытаться отыскать локальный экстремум функции, сдвигая в соответствующую сторону отрезок [a, b], при условии, что параметр x не выйдет за пределы допустимых значений области определения f (х).

После написания программы поиска минимума функции одной переменной следует преобразовать ее в функцию вида

,

возвращающую значение аргумента 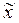, при котором внешная (посылаемая в качестве параметра) функция 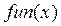достигает наименьшего значения на отрезке :

.

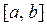Полученную функцию рекомендуется протестировать на некоторых эталонных функциях, например:

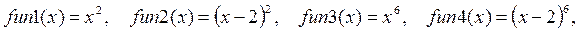
а также гиперболах

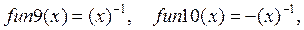
определяя отрезки 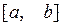как содержащие минимум функции, так и слева и справа от него.

Дата добавления: 2014-12-27