Методы построения функций принадлежности нечетких множеств

Примеры записи нечеткого множества

Пусть Х = { x ₁, x ₂, x ₃, x ₄, x ₅ }, M = [0,1]; A - нечеткое множество, для которого

m _A (x ₁)=0,3;
m _A (x ₂)=0;
m _A (x ₃)=1;
m _A (x ₄)=0,5;
m _A (x ₅)=0,9.

Тогда A можно представить в виде:
A = {0,3/ x ₁; 0/ x ₂; 1/ x ₃; 0,5/ x ₄; 0,9/ x ₅ }, или
A = 0,3/ x ₁ + 0/ x ₂ + 1/ x ₃ + 0,5/ x ₄ + 0,9/ x ₅, или таблицей (табл.1)

Таблица 1

Представление нечеткого множества А

х 1	х 2	х 3	х 4	х 5
0,3			0,5	0,9

Замечание. Здесь знак " + " не является обозначением операции сложения, а имеет смысл объединения.

При построении функций принадлежности используются прямые и косвенные методы. При использовании прямых методов эксперт либо просто задает для каждого x Î Х значение m _A (x), либо определяет функцию совместимости. Как правило, прямые методы задания функции принадлежности используются для измеримых понятий, таких как скорость, время, расстояние, давление, температура и т.д., или когда выделяются полярные значения.

Во многих задачах при характеристике объекта можно выделить набор признаков и для каждого из них определить полярные значе-ния, соответствующие значениям функции принадлежности 0 или 1.

Например в задаче распознавания лиц можно выделить следующие шкалы (табл. 2)

Таблица 2

Шкалы в задаче распознавания образов

x 1	высота лба	низкий	широкий
x 2	профиль носа	курносый	горбатый
x 3	длина носа	короткий	длинный
x 4	разрез глаз	узкие	широкие
x 5	цвет глаз	светлые	темные
x 6	форма подбородка	остроконечный	квадратный
x 7	толщина губ	тонкие	толстые
x 8	цвет лица	темный	светлый
x 9	очертание лица	овальное	квадратное

Для конкретного лица А эксперт, исходя из приведенной шкалы, задает m _A (x) на [0,1], формируя векторную функцию принадлеж-ности { m _A (x ₁), m _A (x ₂), ..., m _A (x ₉)}.

При построении функций принадлежности используются также групповые прямые методы, когда, например, группе экспертов предъявляют конкретное лицо, и каждый должен дать один из двух ответов: «этот человек лысый» или «этот человек не лысый», тогда количество утвердительных ответов, деленное на общее число экспертов, дает значение m_{«лысый»} (данного лица).

Введем следующие обозначения: K - количество экспертов; 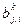- мнение k -го эксперта о наличии у элемента u_j свойств нечеткого множества suppI_j, k =1,…, K, i =1,…, n, j =1,…, m,. Будем считать, что экспертные оценки бинарные, т.е. 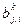Î{ 0,1 }, где 1 (0) указывает на наличие (отсутствие) у элемента u_j свойств нечеткого множества suppI_j. По результатам опроса экспертов, степени принадлежности нечеткому множеству suppI_j, j =1,…, m рассчитываются следующим образом:

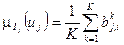, i= 1 ,…,n. (1)

Пример. Построить функции принадлежности значений «низкий», «средний», «высокий», используемых для лингвистической оценки переменной «рост мужчины». Результаты опроса пяти экспертов приведены в табл. 3.

Таблица 3

Результаты опроса экспертов

k	Значения	[160, 165)	[165, 170)	[170, 175)	[175, 180)	[180, 185)	[185, 190)	[190, 195)	[195, 200)
Эксперт 1	низкий
средний
высокий
Эксперт 2	низкий
средний
высокий
Эксперт 3	низкий
средний
высокий
Эксперт 4	низкий
средний
высокий
Эксперт 5	низкий
средний
высокий

Результаты обработки экспертных мнений представлены в табл. 4. Числа курсивом – это количество голосов, отданных экспертами за принадлежность нечеткому множеству соответствующего элемента универсального множества. Числа обычным шрифтом – степени принадлежности, рассчитанные по формуле (1). Графики функций принадлежности показаны на рис. 6.

Таблица 4

Результаты обработки мнений экспертов

Значения	[160, 165)	[165, 170)	[170, 175)	[175, 180)	[180, 185)	[185, 190)	[190, 195)	[195, 200)
низкий	5	4	3	0	0	0	0	0
	0.8	0.6
средний	0	2	4	5	3	2	0	0
	0.4	0.8		0.6	0.4
высокий	0	0	0	1	2	4	5	5
			0.2	0.4	0.8

Рис. 6. Функции принадлежности нечетких множеств из примера

Косвенные методы определения значений функции принадлежности используются в случаях, когда нет элементарных измеримых свойств, через которые определяется нечеткое множество. Как правило, это методы попарных сравнений. Если бы значения функций принадлежности были нам известны, например, m _A (x_i) = w_i, i =1,2,..., n, то попарные сравнения можно представить матрицей отношений A ={ a_ij }, где a_ij = w_i/w_j (операция деления).

На практике эксперт сам формирует матрицу A, при этом предполагается, что диагональные элементы равны 1, а для элементов, симметричных относительно диагонали, a_ij =1 /a_ij, т.е. если один элемент оценивается в a раз сильнее чем другой, то этот последний должен быть в 1/a раз сильнее, чем первый. В общем случае задача сводится к поиску вектора w, удовлетворяющего уравнению вида А_w =l _max w, где l _max - наибольшее собственное значение матрицы A. Поскольку матрица А положительна по построению, решение данной задачи существует и является положительным.

Дата добавления: 2014-12-27