Нечеткие интервалы и a-уровни

В отличие от традиционного подхода к имита­ционному моделированию, при создании нечетко-интервальной модели на первом этапе строится обычная статическая или динамическая модель ис­следуемой системы в предположении детермини­рованности всех ее параметров, т.е. при допуще­нии отсутствия неопределенностей. Далее, в соот­ветствии с принципом нечетко-интервального рас­ширения параметры модели заменяются их нечетко- или четко-интервальными аналогами и выполняют­ся прямые вычисления нечетких интервалов для вы­ходных переменных модели. При этом используют­ся элементы нечетко-интервальной арифметики.

Вычисление значений критерия при нечеткой постановке задачи выбора требует выполнения различных действий над нечеткими переменными.

Применение принципа обобщения Беллмана-Заде сопряжено с двумя трудностями:

· большой объем вычислений – количество элементов результирующего нечеткого множества, которые необходимо обработать, равно P ₁ P ₂… P_n, где P_i – количество точек, на которых задан i -й нечеткий аргумент, i =1,…, n;

· необходимость построения верхней огибающей элементов результирующего нечеткого множества.

Более практичным является применение a-уровневого принципа обобщения. В этом случае нечеткие числа представляются в виде разложений по a-уровневым множествам. Выполнение операций над нечетко-интерваль­ными числами сводится к выполнению опе-раций над их a-уровнями.

Применение a-уровневого принципа обобщения сводится к решению для каждого a-уровня следующей задачи оптимизации: найти максимальное и минимальное значения рассчитываемой функции y при условии, что аргументы могут принимать значения из соответствующих a-уровневых множеств. Количество a-уровней выбирают так, чтобы обеспечить необходимую точность вычислений (рис.11).

Рис. 11. Решение задач с помощью a-уровней

Правила выполнения арифметических операций для положительных нечетких чисел приведены в табл. 6. Эти правила необходимо применять для каждого a-уровня.

Таблица 6

Правила выполнения арифметических операций для положительных нечетких чисел (для каждого a-уровня)

Арифметическая операция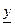

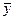
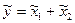
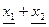
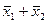
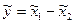
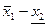
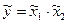
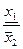
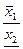
Рассмотрим этот механизм на примере сложения. Пусть существуют нечеткие интервалы А и В, тогда нечеткий интервал С, рав­ный их сумме, можно найти по формуле:

С = А+В= U С _a = U(А _a+ B _a),

где С _a, А _a, B _a – a-уровни нечетких интервалов С, А и В соответственно, т. е. четкие интервалы с одинаковыми значениями функции принадлеж­ности нечеткому интервалу; U – знак объединения по a-уровням.

Дата добавления: 2014-12-27