Нечетко-интервальная арифметика

Операции вычитания, деления и умножения над нечеткими интервалами выполняются анало­гично. В настоящее время существует несколько вариантов интервальной арифметики. В про­стейшем и наиболее распространенном из них со­ответствующие арифметические операции над чет­кими интервалами А= [ А ₁, А ₂] и В= [ В ₁, В ₂] вы­полняются следующим образом (табл.6):

А+В= [ A ₁ +B ₁ ,A ₂ +B ₂];

А-В= [ A ₁ -В ₂ ,А ₂ -В ₁],

А * В=[min (A ₁* B ₁, А ₂* В ₂, А ₁* В ₂, А₂*В ₁), max (A ₁* B ₁, А ₂* В ₂, А ₁* В ₂, А ₂ *B ₁)];

А / В= [ А ₁, А ₂]*[1/ В ₂, 1/ B ₁].

Для поддержки расчетов по экономико-матема­тическим моделям с нечетко-интервальными пара­метрами разработано специальное программное обеспечение, реализованное на языке C++ с ис­пользованием техники объектно-ориентированно­го программирования, позволяющее после задания параметров исходных нечетких интервалов в дальнейшем оперировать с ними как с обычными четкими параметрами в со­ответствии с правилами обычной математики. Разработанное программ­ное обеспечение, расширяя возможно­сти C++, позволяет при разработке экономико-ма­тематической модели представить математические операции с нечеткими интервалами в привычной форме С=А+В, С=А / В и т. д.

Для обоснования адекватности предлагаемого подхода сопоставим результаты, полученные с ис­пользованием a-уровневого принципа обобщения, с результатами традиционного имитационного моделирования типового процесса снабжения потребителя груза­ми из нескольких источников.

2.3 Пример «Задача грузовых перевозок»

Рассмотрим задачу мо­делирования процесса снабжения асфальтобетон­ного завода галькой одновременно из трех карьеров.

Входные параметры: время по­грузки автомобиля, время разгрузки автомобиля, производительность каждого из карьеров, скорость автомобилей и время простоя в мелком ремонте (устранение неисправности в пути самим шофером).

Ср. производительность 10 т/ч

Рис.12. Схема снабжения завода галькой

При использовании традиционного подхода к имитационному моделированию суммарную сред­нюю производительность карьеров примем равной средней производительности завода.

Час­тотные распределения входных параметров зададим нормальными или равномерными, характери­стики распределений (математические ожидания, среднее квадратическое отклонение и пр.) возьмем из нормативной литературы по дорожно­му строительству.

В имитационном моделировании для получе­ния значений входных параметров используются генераторы случайных чисел с соответствующими законами распределения.

В процессе прогонки модели имитируется ра­бота предприятия в течение 1000 рабочих дней, что позволяет получить частотные распределения вы­ходных параметров (суммарное время простоя ав­томобилей на погрузке в карьерах и на заводе, сум­марное время ремонтов автомобилей и пр.) с дос­товерной точностью.

При решении поставленной задачи методом не­четко-интервальной математики вначале по­строим детерминированную балансовую модель про­цесса снабжения завода галькой из трех карьеров:

t ₁ = 2S ₁/q + t_п +t _раз, t ₂ = 2S ₂/q + t_п +t _раз, t ₃= 2S ₃/q + t_п +t _раз,

n ₁ = (t _рд -t ₁) a ₁/60 c; n ₁=(t _рд -t ₂) a ₂/60 c; n ₁=(t _рд -t ₃) a ₃/60 c;

t _перв = 60 min (S ₁ ,S ₂, S ₃)+ t_п+ 60 с / a*min (S ₁ ,S ₂ ,S ₃);

t_пр=t _рд -t _перв-(n ₁+ n ₂+ n ₃) t _раз;

st= 2 st ₀(n ₁ S ₁ +n ₂ S ₂ +n ₃ S ₃);

r=r ₀(S ₁ n ₁/q+ S ₂ n ₂/q+ S ₃ n ₃/q);

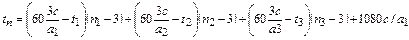t* _раз =max (n ₁, n ₂, n ₃)*[60(2 max (S ₁, S ₂, S ₃)/q-(S ₁, S ₂, S ₃)/q)+3 t _раз]

где S ₁, S ₂, S ₃– расстояния от завода до первого, второго и третьего карьеров соответственно, км; a ₁, a _2, a ₃ ^— производительности первого, второго и третьего карьеров соответственно, т/ч; t_п – время погрузки, мин; t _раз – время разгрузки, мин;

с – грузоподъемность одного грузовика, т; st ₀ - стоимость перевозок, тыс. руб./(т•км); r ₀ – норма­тивный коэффициент ремонта, мин ремонта/ч ра­боты автомобиля; q – скорость автомобиля при перевозке, км/ч; t _рд – продолжительность ра­бочего дня за вычетом времени обеденного пере­рыва, мин; t ₁, t ₂, t ₃ – время, необходимое для по­грузки, перевозки, разгрузки и возвращения в карьер для первого, второго и третьего карьеров со­ответственно, мин; n ₁, n ₂, n ₃ – число рейсов, со­вершаемых за рабочий день из первого, второго и третьего карьеров соответственно; t _перв – время от начала рабочего дня до разгрузки первого авто­мобиля на заводе, мин; t _пр – время простоя заво­да в течение рабочего дня из-за отсутствия галь­ки, мин; st – стоимость перевозок, совершенных за весь рабочий день, тыс. руб.; r – общая про­должительность мелкого ремонта в течение ра­бочего дня, мин; t*_п – общее время простоя авто­мобилей на погрузке и в очереди на погрузку, мин; t* _раз – общее время простоя автомобилей на разгрузке и в очереди на разгрузку, мин.

Для примера рассмотрим результаты расчета суммарной (за один рабочий день) продолжитель­ности ремонтов (рис.13). Частотное распределение суммарной продолжительности ремонтов (на рис. 13 нормировано на 1) было получено при прямом ис­пользовании исходной имитационной модели; со­ответствующие нечеткие интервалы получены при расчете с использованием нечетко-интерваль­ного расширения модели.

Как видно из рис. 13, результаты, полученные с использованием традиционного и нечетко-интер­вального подходов, весьма близки, что говорит о достаточной точности предлагаемой методики. Следует отметить, что наиболее возможное значе­ние, полученное при использовании имитационной модели, может не всегда совпадать с наиболее возможным значением, рассчитанным с примене­нием нечетко-интервальной математики. Расхождение зависит в основном от допуще­ний, принятых при создании балансовой модели. Если балансовая модель точно описывает реальную модель, наиболее возможные значения, полученные при применении различных методов, будут близкими.

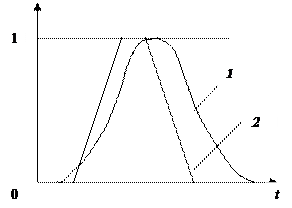Рис.13. Результаты моделирования продолжительности ремонтов (1 – традиционная имитационная модель; 2 – нечетко-интер­вальная модель)

Как свидетельствуют полученные результаты, нечетко-интервальный подход, основанный на не­четко-интервальном расширении детерминиро­ванной балансовой модели исследуемой технико-экономической системы, позволяет получать ре­зультаты практически той же точности, что и пря­мое имитационное моделирование.

В то же время нечетко-интервальный метод мо­делирования реальных процессов обладает рядом преимуществ по сравнению с общепринятым ими­тационным подходом. К этим преимуществам от­носятся:

· возможность моделирования в случаях со слож­ным частотным распределением исходных па­раметров или неизвестным частотным распре­делением (в последнем случае можно использо­вать нечеткие интервалы, построенные на осно­ве экспертных оценок);

· значительная экономия машинного времени и ресурсов;

· простота в использовании;

· большая гибкость (при изменении реальной мо­дели достаточно изменить формулы расчета);

· возможность учитывать маловероятные события и крайние значения случайных переменных;

· возможность напрямую ставить и решать опти­мизационные задачи с использованием нечетко-интервальных расширений соответствующих детерминированных постановок этих задач.

Дата добавления: 2014-12-27