
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Ньютона решения систем нелинейных уравнений
|
|
|
|
Упражнения.
4.5 Методом простой итерации решить с точностью до ε= 0,001 систему линейных алгебраических уравнений:
а) 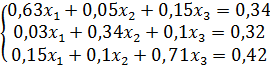 ; б)
; б) 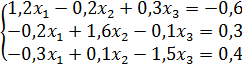 ; в)
; в) 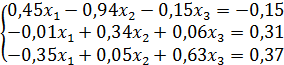 ; г)
; г) 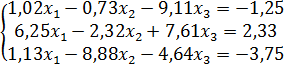 ; д)
; д) 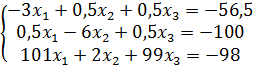 ; е)
; е) 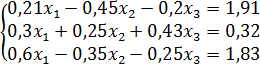 .
.
4.6 Методом Зейделя решить с точностью до ε= 0,001 систему линейных алгебраических уравнений:
а) 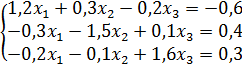 ; б)
; б) 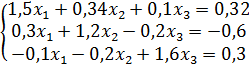 ; в)
; в) 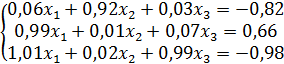 ; г)
; г) 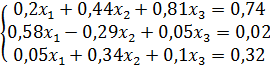 ; д)
; д) 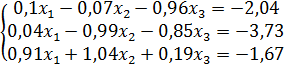 ; е)
; е) 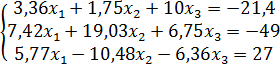 .
.
Часто при решении прикладных задач возникает необходимость решать системы нелинейных уравнений. Пусть
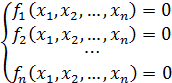 , (65)
, (65)
где 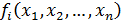 ,
, 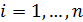 , – функции действительных переменных
, – функции действительных переменных 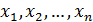 – система n нелинейных уравнений с n неизвестными. Обозначим за
– система n нелинейных уравнений с n неизвестными. Обозначим за 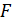 отображение n -мерного вещественного пространства
отображение n -мерного вещественного пространства 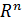 самого себя, т.е.
самого себя, т.е. 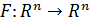 заданного по правилу
заданного по правилу 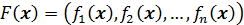 , где
, где 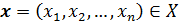 . Тогда систему (65) можно записать в операторном виде:
. Тогда систему (65) можно записать в операторном виде:
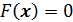 . (66)
. (66)
Для решения системы (66) обычно используют итерационные методы. Как и в случае с СЛАУ для систем нелинейных уравнений эти методы подразделяются на явные, неявные и стационарные.
Каноническая форма записи итерационного метода решения системы (66) аналогично канонической форме (46) итерационного метода решения СЛАУ
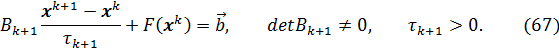
Запишем его в виде
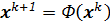 , (68)
, (68)
при это операторное уравнение (66) примет вид
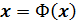 ,
,
где 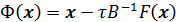 .
.
Таким образом, решение уравнения (66) сводится к решению уравнения 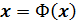 , т.е. к отысканию неподвижной[20] точки отображения Ф. С подобной задачей мы уже сталкивались в процессе построения приближенного решения уравнений с одной неизвестной (см. п. 2.2.4.). Она решается на основе теоремы, сформулированной в п. 2.2.4. Аналогичное утверждение верно и для многомерного случая.
, т.е. к отысканию неподвижной[20] точки отображения Ф. С подобной задачей мы уже сталкивались в процессе построения приближенного решения уравнений с одной неизвестной (см. п. 2.2.4.). Она решается на основе теоремы, сформулированной в п. 2.2.4. Аналогичное утверждение верно и для многомерного случая.
Теорема (принцип сжимающих отображений для систем уравнений). Пусть отображение Ф, определенное на множестве
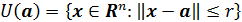 ,
,
является сжимающим[21] на этом множестве с коэффициентом сжатия q, причем
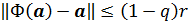 .
.
Тогда в 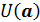 отображение Ф имеет единственную неподвижную точку х * и итерационный метод (68) сходится к х * при любом начальном приближении
отображение Ф имеет единственную неподвижную точку х * и итерационный метод (68) сходится к х * при любом начальном приближении 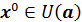 , причем для погрешности справедливы оценки
, причем для погрешности справедливы оценки
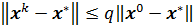 ,
,
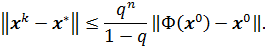
Одним из итерационных методов решения систем (66) является метод Ньютона. Он имеет следующую схему
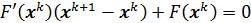 .
.
Таким образом, чтобы получить метод Ньютона, в (67) нужно положить 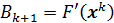 и
и 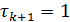 , при этом необходима обратимость матриц
, при этом необходима обратимость матриц 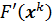 . Метод Ньютона можно записать и в другом виде
. Метод Ньютона можно записать и в другом виде
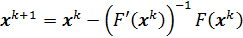 .
.
Если начальное приближение 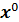 достаточно близко к решению системы, то он сходится со вторым порядком.
достаточно близко к решению системы, то он сходится со вторым порядком.
Глава 5. Численное интегрирование.
5.1. Формула Ньютона-Лейбница [22] и численное интегрирование.
Из курса математического анализа вы знакомы с вычислением определенных интегралов с помощью формулы Ньютона-Лейбница:
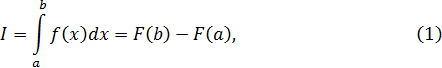
где 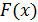 – любая первообразная подынтегральной функции
– любая первообразная подынтегральной функции 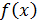 на отрезке
на отрезке 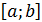 . Формула Ньютона-Лейбница играет важную роль, устанавливая связь задачи определенного интегрирования с задачей отыскания первообразной (задачей неопределенного интегрирования). Она позволяет вычислять интегралы от элементарных функций, первообразные которых тоже являются элементарными функциями. Например,
. Формула Ньютона-Лейбница играет важную роль, устанавливая связь задачи определенного интегрирования с задачей отыскания первообразной (задачей неопределенного интегрирования). Она позволяет вычислять интегралы от элементарных функций, первообразные которых тоже являются элементарными функциями. Например,
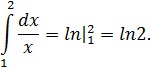
Однако существует много простых функций, первообразные которых не выражаются через элементарные функции. Например, для функций 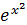 и
и 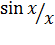 первообразные нельзя выразить с помощью элементарных функции. Поэтому описанный выше способ вычисления определенного интеграла для этих функций неприменим. Формула Ньютона-Лейбница не позволяет также вычислить интегралы от функций заданных графически или таблично. То есть она не дает общего, универсального метода нахождения определенного интеграла от произвольной функции
первообразные нельзя выразить с помощью элементарных функции. Поэтому описанный выше способ вычисления определенного интеграла для этих функций неприменим. Формула Ньютона-Лейбница не позволяет также вычислить интегралы от функций заданных графически или таблично. То есть она не дает общего, универсального метода нахождения определенного интеграла от произвольной функции 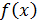 по ее значениям на отрезке
по ее значениям на отрезке 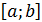 , а значит и не является алгоритмом решения задачи определенного интегрирования.
, а значит и не является алгоритмом решения задачи определенного интегрирования.
Универсальные алгоритмы вычисления определенных интегралов дают формулы численного интегрирования или, как их обычно называют, квадратурные формулы [23] Квадратурные формулы имеют вид
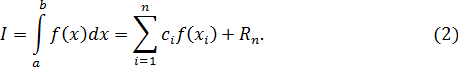
В формуле (2) точки 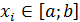 называются узлами, коэффициенты
называются узлами, коэффициенты 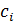 – весовыми множителями или весами, величину
– весовыми множителями или весами, величину 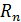 – остаточным членом или погрешностью. Узлы и веса подбираются таким образом, чтобы
– остаточным членом или погрешностью. Узлы и веса подбираются таким образом, чтобы

Выполнение предельного равенства (3) означает, что если в квадратурной формуле (2) пренебречь остаточным членом 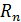 , то получится приближенное равенство
, то получится приближенное равенство
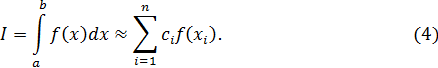
Если выполняется равенство (3), то справедливо условие

которое называют сходимостью. Оно позволяет сделать погрешность в равенстве (4) меньше любого наперед заданного числа за счет выбора количества узлов. Таким образом, можно вычислять интеграл I с любой наперед заданной точностью. Но чем выше требования точности, тем больше слагаемых следует удерживать в сумме. За точность приходится платить увеличением объема вычислений.
В этой главе мы рассмотрим три основных квадратурных формулы – формула прямоугольников, формула трапеции и формула Симпсона[24] (парабол) и рассмотрим проблему их точности.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 935; Нарушение авторских прав?; Мы поможем в написании вашей работы!